電験三種 H27年 理論 問17 問題と解説

　問 題　　　　　

図のようなV結線電源と三相平衡負荷とからなる平衡三相回路において、R=5Ω、L=16mHである。また、電源の線間電圧e_a[V]は、時刻t[s]においてと表され、線間電圧e_b[V]はe_a[V]に対して振幅が等しく、位相が120°遅れている。ただし、電源の内部インピーダンスは零である。このとき、次の(a)及び(b)の問に答えよ。

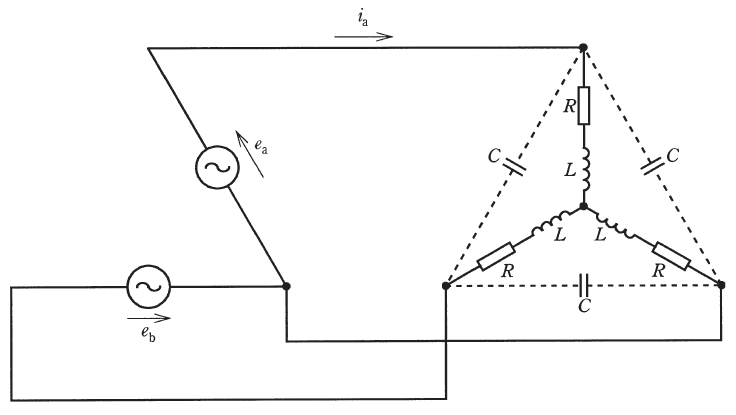
(a)　図の点線で示された配線を切断し、3個のコンデンサを三相回路から切り離したとき、三相電力Pの値[kW]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 1
2. 3
3. 6
4. 9
5. 18

(b)　点線部を接続することによって同じ特性の3個のコンデンサを接続したところi_aの波形はe_aの波形に対して位相が30°遅れていた。このときのコンデンサCの静電容量の値[F]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 3.6×10^-5
2. 1.1×10^-4
3. 3.2×10^-4
4. 9.6×10^-4
5. 2.3×10^-3

 

 

 

 

 

　解 説　　　　

(a)

(a)ではコンデンサについては考えなくてよいので、抵抗とコイルを1相分だけ抜き出して等価回路を描くと、次の図のようになります。

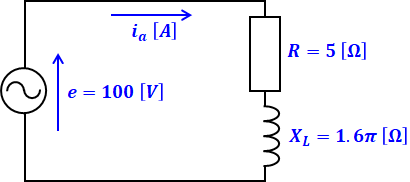
上図のR=5[Ω]は問題文そのままですが、コイルのリアクタンスX_L=1.6π[Ω]については以下の式から算出しています(ω=100πとしているのは、e_aの式のsinの(　)内の値がωtと等しいためです)。

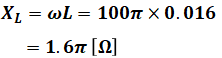
また、1相あたりの電源電圧e=100[V]は以下のように算出しています。まず、e_aの式の頭の部分100√6が最大電圧に等しく、実効電圧はこれの√2分の1倍となります。さらに、三相回路を中性点で切って1相分の等価回路としているため、電源電圧は線間電圧の√3分の1倍になります。

よって、次の計算式の通り、eは100[V]とわかります。

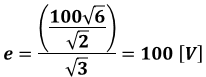
以上より、この等価回路を流れる電流i_a[A]は、次のように計算することができます。

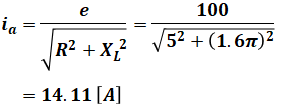
よって、求める三相電力Pの値は次の通りとなります(三相分なので最初に3を掛けています)。

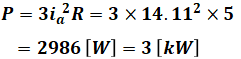
(b)

問題文には「i_aの波形はe_aの波形に対して位相が30°遅れていた」とありますが、一方、三相回路においてY結線の相電圧eは線間電圧e_aよりも位相が30°遅れます。よって、負荷側をY結線で表せば、線電流i_aと相電圧eが同位相(位相差なし)ということになります。

ここで、(a)と同様に1相分の等価回路を描くと次のようになります。ちなみに、コンデンサは抵抗とコイルと合わせるためにΔ結線からY結線に変換していて、その変換により、コンデンサのリアクタンスを1/3倍(=コンデンサの静電容量を3倍)しています。

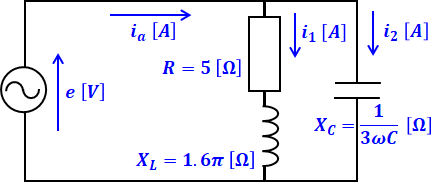
上図を見ながらi_aを式で表すと、次のように表すことができます。

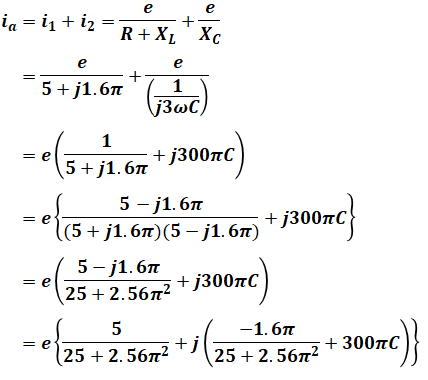
ここで、上記の通りi_aとeとの位相差が0なので、上式の虚数部が0になるはずです。

よって、

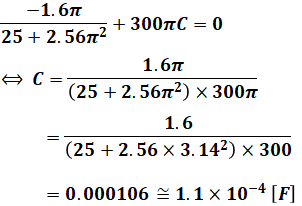
と計算することで、コンデンサの静電容量Cが算出できます。