問 題
図のように、真空中で2枚の電極を平行に向かい合せたコンデンサを考える。各電極の面積をA[m2]、電極の間隔をl[m]とし、端効果を無視すると、静電容量は( ア )[F]である。このコンデンサに直流電圧源を接続し、電荷Q[C]を充電してから電圧源を外した。
このとき、電極間の電界E=( イ )[V/m]によって静電エネルギーW=( ウ )[J]が蓄えられている。この状態で電極間隔を増大させると静電エネルギーも増大することから、二つの電極間には静電力の( エ )が働くことが分かる。
ただし、真空の誘電率をε0[F/m]とする。
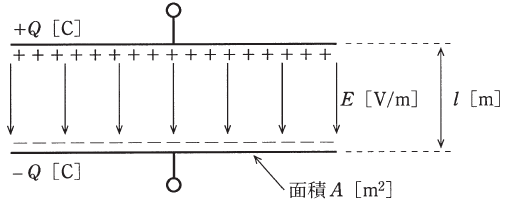
上記の記述中の空白箇所(ア)、(イ)、(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
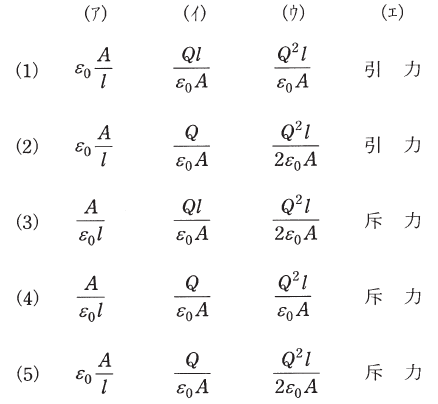
正解 (2)
解 説
この問題の( ア )と( イ )については、問1で紹介した静電容量の式、電荷の式、電界の式を使います。
![]()
- C:静電容量[F]
- ε:極板間の誘電率[F/m]
- A:極板の面積[m2]
- d:極板間の距離[m]
![]()
- Q:電荷[C]
- V:電圧[V]
![]()
今回の問題ではεがε0、dがlで示されているので、( ア )には「ε0A/l」が入ります。
また、電界の式に静電容量の式と電荷の式を代入することで、Eは次のように式変形できます。
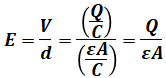
よって、( イ )には「Q/ε0A」が入ります。
また、静電エネルギーは次のように計算でき、( ウ )が求められます。
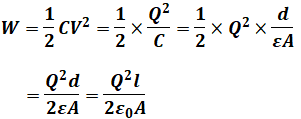
最後の( エ )について、+の電気と-の電気は引き合うので「引力」が入ります。+の電気同士や-の電気同士であれば、反発する力(斥力)となります。

コメント