問 題
図に示すように、フィードバック接続を含んだブロック線図がある。このブロック線図において、T=0.2s、K=10としたとき、次の(a)及び(b)の問に答えよ。
ただし、ωは角周波数[rad/s]を表す。
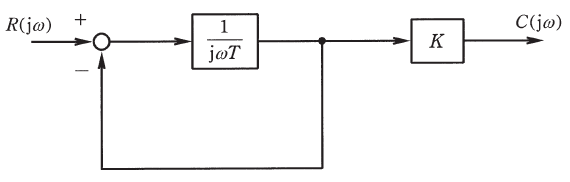
(a) 入力をR(jω)、出力をC(jω)とする全体の周波数伝達関数W(jω)として、正しいものを次の(1)～(5)のうちから一つ選べ。
(b) 次のボード線図には、正確なゲイン特性を実線で、その折線近似ゲイン特性を破線で示し、横軸には特に折れ点角周波数の数値を示している。上記(a)の周波数伝達関数W(jω)のボード線図のゲイン特性として、正しいものを次の(1)～(5)のうちから一つ選べ。
ただし、横軸は角周波数ωの対数軸であり、-20[dB/dec]とは、ωが10倍大きくなるに従って｜W(jω)｜が-20dB変化する傾きを表している。
解 説
(a)
フィードバックの伝達関数はこの分野で最も重要なので、この式は公式としてぜひ覚えておきたいところです。下図の左側のようなフィードバックモデルは右側のように簡略化できるので、入力をX(s)、出力をY(s)として式化すると、
となります。図中の「∓」が、式では「±」とひっくり返ることに注意してください。
今回の問題にこれを適用すると、
で、G2の位置にはブロックが何もないので、G2=1となります。よって、フィードバック結合によってできる式は、
となり、さらに右側のブロック(K)との直列結合になるため、このブロック線図の最終的な伝達関数は、
と表すことができます。
(b)
最初に確認しておきたいのは、ゲイン特性は以下の式で表されるということです。
- g：ゲイン[dB]
よって、上式に(a)での計算結果を代入すると、
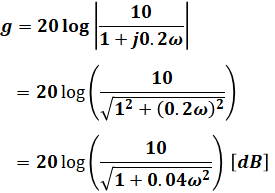
となります。この式をグラフ化した選択肢が正解となります。
ここで、試しにω=0を代入してみると、
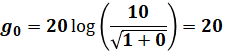
となるので、正解の選択肢は(1)か(2)に限られます。(1)と(2)の違いは、真ん中あたりの変曲点がω=5であるか、ω=0.2であるかなのですが、折れ点角周波数ωは、
と計算することができるため、正解は(1)だとわかります。
もし折れ点角周波数ωの式が思い出せなくても、上記で求めたゲインgの式にω=5やω=0.2を代入して得られる結果と、選択肢のグラフとを照らし合わせれば、正解を選ぶことはできます(以下ではω=5とω=0.2の両方を試していますが、実際にはどちらか一方で充分です)。
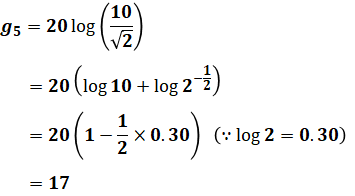
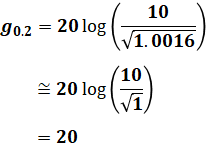
以上から、(1)と(2)とでは、(1)のグラフのほうが正しいと判断することが可能です。
コメント