問 題
図のように、真空中において二つの小さな物体A、Bが距離r[m]を隔てて鉛直線上に置かれている。Aは固定されており、Aの真下にBがある。物体A、Bはそれぞれ、質量mA[kg]、mB[kg]をもち、電荷+qA[C]、-qB[C]を帯びている。qA>0、qB>0とし、真空の誘電率をε0[F/m]とする。次の(a)及び(b)の問に答えよ。
ただし、小問(a)においては重力加速度g[m/s2]の重力を、小問(b)においては無重力を、それぞれ仮定する。物体A、Bの間の万有引力は無視する。
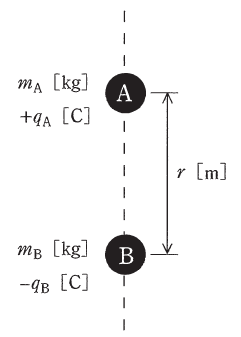
(a) 重力加速度g[m/s2]の重力のもとでBを初速度零で放ったとき、BはAに近づくように上昇を始めた。このときの条件を表す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
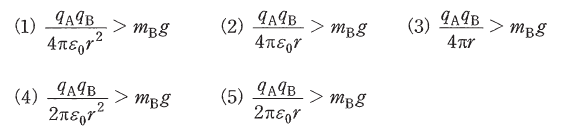
(b) 無重力のもとでBを下向きの初速度vB[m/s]で放ったとき、Bは下降を始めたが、途中で速度の向きが変わり上昇に転じた。このときの条件を表す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
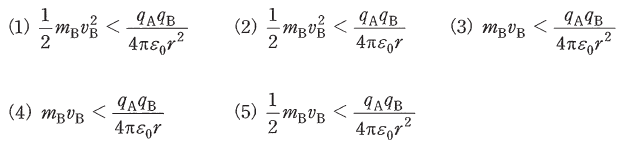
解 説
(a)
物体AとBはそれぞれ正電荷と負電荷を帯びているので、これらの間には引力が働きます。引力の大きさを表す式は以下の通りです。
![]()
- F:静電気力(斥力または引力)[N]
- ε0:真空の誘電率[F/m]
- q:電荷[C]
- r:電荷間の距離[m]
これが物体Bに働く重力の大きさmBg[N]よりも大きければ、物体Bは物体Aに近づきます(ちなみに、物体Aは固定されているので、物体Aの重力については考える必要がありません)。
よって、BがAに近づく条件は、
![]()
となります。
(b)
(b)では無重力条件下なので、(a)と違って重力による影響はありませんが、その代わりにBに初速度が加わります。
最初は初速が速いのでBは下降(無重力なので下降というよりもAから離れていくだけですが)しますが、最初の時点で外からBに与えられた運動エネルギーよりも、やはり最初の時点でAの位置を基準としたBの静電エネルギー(電荷の位置エネルギー)のほうが大きければ、Bは途中からA側へ引っ張られることになります。
Bに外から与えられた運動エネルギーは![]() で、静電エネルギーは「力×距離」より
で、静電エネルギーは「力×距離」より
![]()
なので、Bが途中で上昇に転じる条件は、
![]()
となります。

コメント