問 題
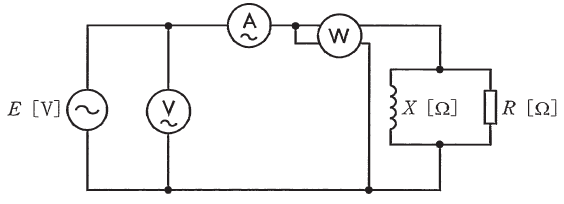
図のように、正弦波交流電圧E[V]の電源が誘導性リアクタンスX[Ω]のコイルと抵抗R[Ω]との並列回路に電力を供給している。この回路において、電流計の指示値は12.5A、電圧計の指示値は300V、電力計の指示値は2250Wであった。
ただし、電圧計、電流計及び電力計の損失はいずれも無視できるものとする。次の(a)及び(b)の問に答えよ。
(a) この回路における無効電力Q[var]として、最も近いQの値を次の(1)~(5)のうちから一つ選べ。
- 1800
- 2250
- 2750
- 3000
- 3750
(b) 誘導性リアクタンスX[Ω]として、最も近いXの値を次の(1)~(5)のうちから一つ選べ。
- 16
- 24
- 30
- 40
- 48
正解 (a)-(4), (b)-(3)
解 説
(a)
無効電力を求める問題なので、有効電力と皮相電力がわかれば、三平方の定理より計算できます。有効電力Pは、電力計の指示値から2250[W]とわかっています。皮相電力Sは、電圧計と電流計の指示値から、S=300×12.5=3750[W]となります。
よって、無効電力Qは、
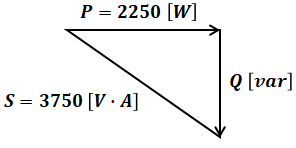
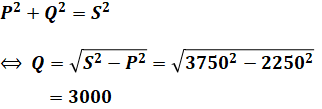
と計算することができます。
(b)
皮相電力のうち、有効電力は抵抗で消費され、無効電力はコイルとコンデンサで消費されます。この問題ではコンデンサがないので、コイルについてだけ考えます。
コイルを流れる電流をIL[A]とすると、コイルの両端の電圧E[V]と誘導性リアクタンスX[Ω]を用いると、
![]()
と表すことができます。
また、EとILとの積が無効電力Qとなるので、誘導性リアクタンスXは次のように計算することができます。
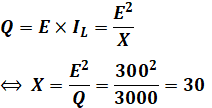

コメント