問 題
交流回路に関する記述として、誤っているものを次の(1)～(5)のうちから一つ選べ。
ただし、抵抗R[Ω]、インダクタンスL[H]、静電容量C[F]とする。
- 正弦波交流起電力の最大値をEm[V]、平均値をEa[V]とすると、平均値と最大値の関係は、理論的に次のように表される。
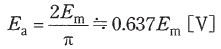
- ある交流起電力の時刻t[s]における瞬時値が、e=100sin100πt[V]であるとすると、この起電力の周期は20msである。
- RLC直列回路に角周波数ω[rad/s]の交流電圧を加えたとき、
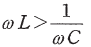の場合、回路を流れる電流の位相は回路に加えた電圧より遅れ、
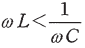の場合、回路を流れる電流の位相は回路に加えた電圧より進む。 - RLC直列回路に角周波数ω[rad/s]の交流電圧を加えたとき、
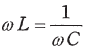の場合、回路のインピーダンスZ[Ω]は、Z=R[Ω]となり、回路に加えた電圧と電流は同相になる。この状態を回路が共振状態であるという。 - RLC直列回路のインピーダンスZ[Ω]、電力P[W]及び皮相電力S[V・A]を使って回路の力率cosθを表すと、
、
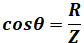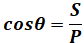の関係がある。
解 説
(1)について、交流起電力の平均値は選択肢の通り、最大値の2/π倍となります。これは知識として覚えておいてもよいですし、正弦波の0からπまでの範囲の総面積(積分値)を求め、それをπで割ることで平均値を求めてもよいです。後者のように計算で求める場合、その計算過程は次のようになります。
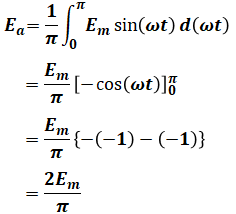
(2)について、交流起電力次の式で表されます。
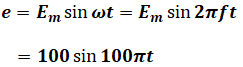
よって、周波数fは2f=100よりf=50[Hz]と求められます。周期T[s]はfの逆数なので、以下のように計算すると、T=20[ms]となって(2)は正しいことがわかります。
(3)について、コンデンサを流れる電流は電圧よりも90°進み、コイルを流れる電流は電圧よりも90°遅れるので、(3)の記述も正しいです。
(4)について、共振状態では記述の通り、コイルとコンデンサのリアクタンスの大きさが同じで向きが反対なので、これらは互いに打ち消し合います。RLC直列回路のインピーダンスZは抵抗RとコイルのリアクタンスXLとコンデンサのリアクタンスXCの3つの合力ですが、このうちXLとXCの和が0になるので、この共振状態ではZ=Rとなるので、(4)は正しいです。
(5)について、皮相電力S[V・A]は有効電力P[W]と無効電力Q[var]の合力です。また、インピーダンスZ[Ω]は(4)の解説の通り、抵抗R[Ω]とコイルのリアクタンスXL[Ω]とコンデンサのリアクタンスXC[Ω]の3つの合力です。ベクトル図で示すと以下のようになるため、力率cosθは
のように表すことができ、(5)の記述が誤りであることがわかります。
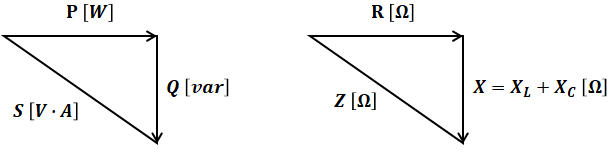
コメント