電験三種 H26年 理論 問1 問題と解説

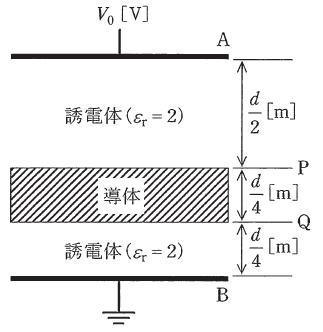
　問 題　　　　　

極板A-B間が比誘電率ε_r=2の誘電体で満たされた平行平板コンデンサがある。極板間の距離はd[m]、極板間の直流電圧はV_o[V]である。極板と同じ形状と大きさをもち、厚さがd/4[m]の帯電していない導体を図に示す位置P-Q間に極板と平行に挿入したとき、導体の電位の値[V]として、正しいものを次の(1)～(5)のうちから一つ選べ。

ただし、コンデンサの端効果は無視できるものとする。

 

 

 

 

 

　解 説　　　　

コンデンサが直列に並んでいるとき、各々のコンデンサの電荷Qは等しくなります。これは、今回のように1つのコンデンサがいくつかの層に分かれているときも同様に考えることができます。また、静電容量C、電位差V、電荷Qの関係式は

より、Qが一定であれば、2つのコンデンサのCを比較することで、Vの比もわかります(Vの比はCの比の逆数となります)。

問題文の図のようにP-Q間に導体を入れるとその部分はコンデンサではなく、ただの導線と同じ扱いになるので、問題文の図は次のように書き換えることができます。

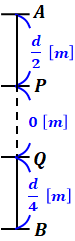
ここで、AP間の静電容量C_APとQB間の静電容量C_QBは次のように表されます。

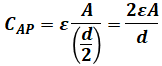
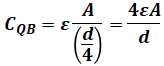
よって、C_AP：C_QB=2：4=1：2となるので、電位差はV_AP：V_QB=2：1となります。つまり、AB間の電位差がV₀[V]、PQ間の電位差が0[V]なので、

となり、求めるPQ間の電位はV₀[V]からV_AP[V]を引くか、あるいは0[V]からV_QB[V]を足せばいいので、いずれにしても、選択肢(4)が正しいことがわかります。