問 題
均等放射の球形光源(球の直径は30cm)がある。床からこの球形光源の中心までの高さは3mである。また、球形光源から放射される全光束は12000lmである。次の(a)及び(b)の問に答えよ。
(a) 球形光源直下の床の水平面照度の値[lx]として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、天井や壁など、周囲からの反射光の影響はないものとする。
- 35
- 106
- 142
- 212
- 425
(b) 球形光源の光度の値[cd]と輝度の値[cd/m2]との組合せとして、最も近いものを次の(1)~(5)のうちから一つ選べ。
光度 輝度
- 1910 1010
- 955 3380
- 955 13500
- 1910 27000
- 3820 13500
解 説
(a)
照度が問われていますが、照度E[lx]は光束F[lm]を面の面積A[m2]で割ったものです。
Fはすでに問題文で与えられていて、Aについては球の中心と観測点との距離が3[m]であるため、半径3[m]の円の表面積と考えればよいので、次のような計算によって算出することができます。
![]()
よって、正解は(2)です。
(b)
1つ目は光度ですが、光度I[cd]は光束F[lm]を立体角ω[sr]で割ったものです。また、ωは面積Sを半径rの2乗で割ったものとなりますが、今回のように面積が球まるまる1つ分であれば、Sは(a)で計算したAと全く同じになるので、計算式は以下のようになります。
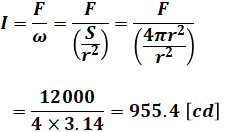
2つ目は輝度ですが、輝度L[cd/m2]は問題文にある単位を見てもわかるように、光度I[cd]を面積A'[m2]で割ったものとなります。ただし注意したいのが、ここでのA’は観測点から光源を見たときの見かけの面積になります。または投影面積と考えても一緒なので、どちらか考えやすいほうで大丈夫です。
今回の場合は直径30cmの球を真下から見ているので、その面積A’は半径15cmの円の面積と同等です。よって、Lは次のように計算されます。
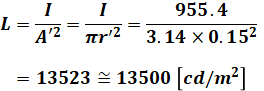
よって、正解は(3)です。

コメント