問 題
次の文章は、三相誘導電動機の等価回路に関する記述である。
三相誘導電動機の1相当たりの等価回路は、( ア )と同様に表すことができ、その等価回路を使用することによって電圧V及び周波数fを同時に変化させるインバータで運転したときの磁束、トルクの特性を検討することができる。
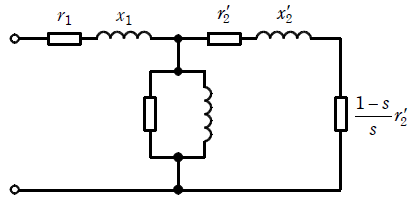
図の( イ )等価回路において、誘導電動機を例えば定格周波数、定格電圧の数パーセント程度の周波数、電圧で始動するときの特性を考える。この場合、もし始動電流が定格電流と同じだけ流れると、( ウ )による電圧降下の一次電圧に対する比率が定格時よりも大きくなるので、磁束が減少し、発生トルクが( エ )することが理解できる。
また、誘導電動機を例えば定格周波数、定格電圧で運転するときは、上記電圧降下による計算誤差が小さく、計算が簡単になるので、励磁回路を図の( オ )側に移した簡易等価回路を使うことも有効である。
この運転では、もしインバータが出力する電圧Vが減少したとしても、V/f比を一定に保つように周波数fを減少させれば、負荷変動に影響されずに励磁電流がほぼ一定となることが分かる。
上記の記述中の空白箇所(ア)、(イ)、(ウ)、(エ)及び(オ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
(ア) (イ) (ウ) (エ) (オ)
- 同期電動機 L形 一次抵抗 増加 右端の負荷抵抗
- 変圧器 T形 一次抵抗 減少 左端の端子
- 同期電動機 T形 二次漏れリアクタンス 減少 右端の負荷抵抗
- 変圧器 L形 一次抵抗 増加 右端の負荷抵抗
- 変圧器 T形 二次漏れリアクタンス 減少 左端の端子
解 説
( ア )について、三相誘導電動機の等価回路は「変圧器」の等価回路と同じように描くことができます。
また、( イ )には「L形」か「T形」が入りますが、これは3組の「抵抗+リアクタンス」の並び方で決まります。問題文に載っている等価回路では、3組の「抵抗+リアクタンス」が左上・右上・下のT字に並んでいるので、これは「T形」等価回路だと判断することができます。
一方、L形等価回路は以下のように、3組の「抵抗+リアクタンス」がL字(Lを時計回りに90°廻した感じ)に並んでいます。
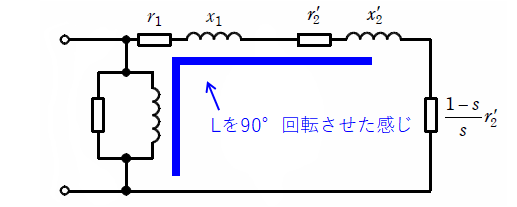
( ウ )について、問題文の図(上図のL形じゃなくて問題文のT形のほうです)を見てもわかるように、一次抵抗はr1のことで、二次抵抗はr2‘と(1-s)/s・r2‘の和のことです。二次抵抗を先にまとめておくと、
![]()
となります。ここで、始動時は滑りs=1であり、徐々に下がっていき、定格運転時にはほぼs=0となります。よって、先ほど計算した二次抵抗は分母にsがあるので、始動時ほど抵抗が小さく、定格時には大きくなります。
つまり、始動時は定格時に比べて二次抵抗が小さい → 一次抵抗による電圧降下が相対的に大きい、ということになるので、( ウ )には「一次抵抗」が入ります。
( エ )は( ウ )から文章がつながっていますが、まず下図を見てください。
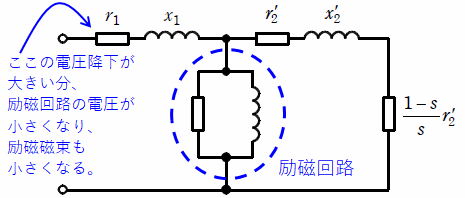
このように、一次抵抗による電圧降下が大きくなるということは、励磁回路での電圧が小さくなることを意味します。また、電圧が小さくなれば励磁磁束も減りますが、ここまでは問題文にも書いてある通りです。
そして、トルクは励磁電流と励磁磁束にそれぞれ比例するため、励磁磁束が減少すればその分トルクも減少します。よって、( エ )には「減少」が入ります。
残る( オ )は、( イ )に関連しますが、結論から先に示すと「左端の端子」となります。現状ではT形等価回路となっていますが、定格運転時はL形等価回路とすることで、計算を簡単化することができます。もしも励磁回路を右端の負荷抵抗側に移すと、すでにある負荷抵抗と重なってしまうので計算が余計複雑になってしまいます。

コメント