電験三種 H25年 理論 問9 問題と解説

　問 題　　　　　

図1のように、R[Ω]の抵抗、インダクタンスL[H]のコイル、静電容量C[F]のコンデンサからなる並列回路がある。この回路に角周波数ω[rad/s]の交流電圧ｖ[V]を加えたところ、この回路に流れる電流はi[A]であった。

電圧v[V]及び電流i[A]のベクトルをそれぞれ電圧[V]と電流[A]とした場合、両ベクトルの関係を示す図2(ア、イ、ウ)及びv[V]とi[A]の時間t[s]の経過による変化を示す図3(エ、オ、カ)の組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

ただし、R≫ωL及びとし、一切の過渡現象は無視するものとする。

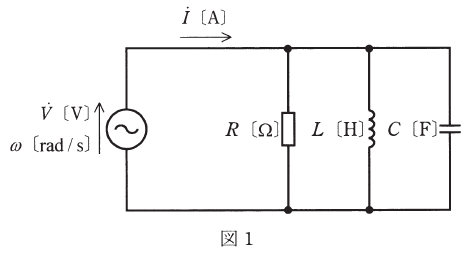
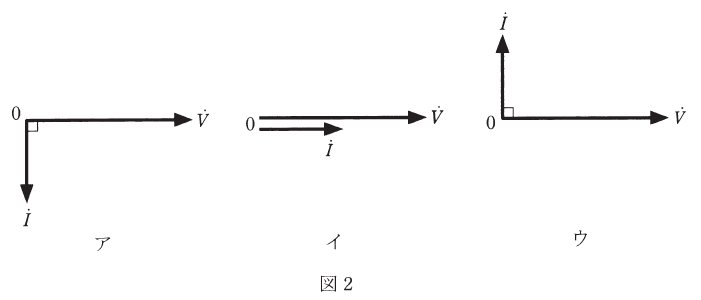
　　図2　　図3

1. ア　　オ
2. ア　　カ
3. イ　　エ
4. ウ　　オ
5. ウ　　カ

 

 

 

 

 

　解 説　　　　

まず、電流はそれぞれ抵抗とインダクタンスとコンデンサへと分かれるので、それぞれに流れる電流をI_R、I_L、I_Cとします。ただし、問題文の最後に「R≫ωL」とあるので、実は抵抗には電流が流れません。よって、I_R=0となり、I_LとI_Cだけを考えれば良いことになります。

ここで、インダクタンスに流れる電流は電圧に対してπ/2だけ遅れ、コンデンサに流れる電流は電圧に対してπ/2だけ進みます。問題文よりなので、I_L：I_C=1：2であることがわかるので、図2の前段階は以下の図のようになります。

ここでI_LとI_Cを合成すれば、図2のウと同じ図になるので、これが正解です。アだとI_LのほうがI_Cよりも大きくなってしまっていますし、イだと位相差がないので、I_Rが流れることになってしまいます。

また、図3を見ると、エは電流と電圧の位相差がないので誤りです。オは電流が電圧に対してπ/2だけ遅れてしまっているのでこれも違います。カだと電流が電圧に対してπ/2だけ進んでいるので、これが正しいです。

以上から、正解は(5)になります。