電験三種 H25年 理論 問6 問題と解説

　問 題　　　　　

図の直流回路において、抵抗R=10[Ω]で消費される電力[W]の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 0.28
2. 1.89
3. 3.79
4. 5.36
5. 7.62

 

 

 

 

 

　解 説　　　　

この問題ではテブナンの定理を使います。問われているのは抵抗R=10[Ω]で消費される電力[W]の値なので、まずはR=10[Ω]の抵抗をないものと考え(=開放して)、下図のV₁とV₂をそれぞれ求めます。

V₁のほうは、60[V]の電源に40[Ω]の抵抗が2つ直列に並んでいて、そのうち片方の電圧を求めればよいので、次の(1)式のようになります。

となり、同様にV₂は以下の(2)式の通りです。

よって、点aと点bでの電圧差V_ab(＝抵抗Rの端子間電圧)は、次の(3)式で表されます。

次に、同じくテブナンの定理ですが、今度は電源を短絡させます。

すると、上図のようになり、左側、右側それぞれの合成抵抗を求めることができるようになります。

40[Ω]の抵抗が2つの合成抵抗をR₁[Ω]とすると、2つは並列に並んでいるので、次の(4)式のようになります。

同様に、60[Ω]の抵抗が2つの合成抵抗をR₂[Ω]とすると、次の(5)式のように書けます。

さらに、これらを合わせたものは直列回路であり、20[Ω](左側)と10[Ω](真ん中)と30[Ω](右側)が直列につながっているので、5つ全ての合成抵抗の値R_all[Ω]は次のように計算できます。

以上の(3)式と(6)式から、問題で与えられた回路は次のような等価回路に描き換えることができます。

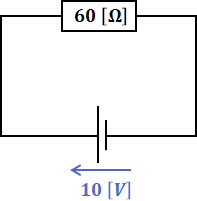
上図より、電流Iはオームの法則より0.1666…となるので、ここでは0.167[A]とします(0.17[A]としても大丈夫です)。よって、R=10[Ω]で消費される電力は次のように算出することができます。

以上から、正解は(1)となります。