問 題
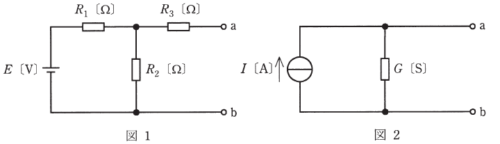
図1のように電圧がE[V]の直流電圧源で構成される回路を、図2のように電流がI[A]の直流電流源(内部抵抗が無限大で、負荷変動があっても定電流を流出する電源)で構成される等価回路に置き替えることを考える。
この場合、電流I[A]の大きさは図1の端子a-bを短絡したとき、そこを流れる電流の大きさに等しい。また、図2のコンダクタンスG[S]の大きさは図1の直流電圧源を短絡し、端子a-bからみたコンダクタンスの大きさに等しい。
I[A]とG[S]の値を表す式の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。

解 説
まず、図1の端子a-bを短絡した図は以下のようになります。

I[A]を求める流れとしては、まず電源を流れる電流I1を求めて、その上で、R2とR3の比から、R3のほうを流れる電流Iを計算します。I1を求めるためには、まず回路全体の抵抗を知る必要があり、そのためにR2とR3の並列な抵抗を合成し、その後、それとR1とは直列に並ぶため、和で合成することができるので、合成抵抗R[Ω]は次のように計算されます。
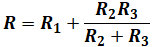
よって、回路全体を流れるI1[A]は次のようになります。

求めるI[A]は、I1のうち、R2ではなくR3を流れる分となるため、比の計算によって求めることができます。
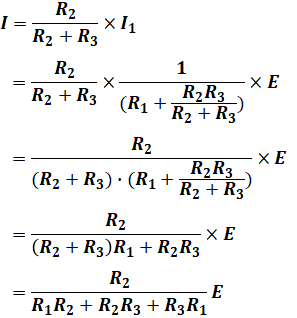
続いて、コンダクタンスG[S]について考えます。
その前にコンダクタンスGについて確認しておきますが、これは[S](ジーメンス)という単位からわかるかもしれませんが、抵抗の逆数です。つまり、[S]とは[Ω-1]と全く同じ単位となります。
ちなみに、抵抗の逆数はアドミタンスY[S]では…?と思う方もいるかもしれませんが、アドミタンスY[S]はインピーダンスZ[Ω]の逆数です。アドミタンスやインピーダンスは抵抗のほかにコイルやコンデンサのリアクタンスも含めた用語ですが、抵抗やコンダクタンスは抵抗分のみを考えて、リアクタンス分については考慮しません。
この問題に関してはそもそも回路中に抵抗しかないので、コンダクタンスと呼んでもアドミタンスと呼んでも同じものを指します。
上記を踏まえて問題文を読むと、コンダクタンスGを求めるためには図1の直流電圧源を短絡し、端子a-bからみればよいとのことなので、以下の図のようになります。
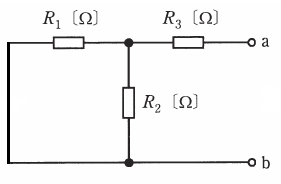
上図において、端子a-bから見た合成抵抗Rは、並列に並んだR1とR2の合成抵抗に対して、R3が直列に接続されていることになるので、次のように計算することができます。
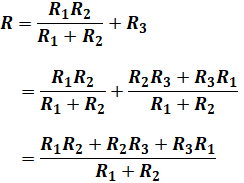
そして、上記で解説したように、この合成抵抗Rの逆数がコンダクタンスGとなるため、求めるGは以下の計算によって求めることができます。
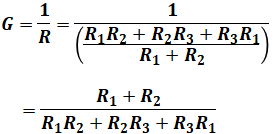
以上から、正解は(2)となります。

コメント