問 題
次の文章は、コイルのインダクタンスに関する記述である。ここで、鉄心の磁気飽和は、無視するものとする。
均質で等断面の環状鉄心に被覆電線を巻いてコイルを作製した。このコイルの自己インダクタンスは、巻数の( ア )に比例し、磁路の( イ )に反比例する。
同じ鉄心にさらに被覆電線を巻いて別のコイルを作ると、これら二つのコイル間には相互インダクタンスが生じる。相互インダクタンスの大きさは、漏れ磁束が( ウ )なるほど小さくなる。それぞれのコイルの自己インダクタンスをL1[H]、L2[H]とすると、相互インダクタンスの最大値は( エ )[H]である。
これら二つのコイルを( オ )とすると、合成インダクタンスの値は、それぞれの自己インダクタンスの合計値よりも大きくなる。
上記の記述中の空白箇所(ア)、(イ)、(ウ)、(エ)及び(オ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。

解 説
( ア )と( イ )に関して、コイルの自己インダクタンスは次の式で表されます。
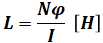
- L:自己インダクタンス[H]
- N:巻数
- φ:磁束[Wb]
- I:電流[A]
しかし、この書き方だと磁路の長さまたは断面積がない上、磁束φは巻数Nに影響するので、上式をさらに変形します。磁束は起磁力Fと磁気抵抗Rを使って、以下のように表すことができます。
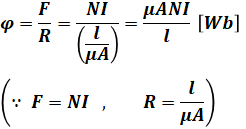
- F:起磁力[A]
- R:磁気抵抗[A/Wb]
- l(エル):磁路の長さ[m]
- μ:透磁率[H/m]
- A:断面積[m2]
よって、上式を先ほどの式に代入すると、
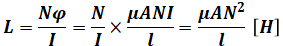
となるので、コイルの自己インダクタンスLは、巻数の2乗に比例して、反比例するのは磁路の長さであるとわかります。よって、( ア )には「2乗」、( イ )には「長さ」が入ります。
( ウ )と( エ )は相互インダクタンスについてですが、相互インダクタンスは次の式で表されます。
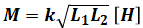
- M:相互インダクタンス[H]
- k:結合係数(0~1)
- L:自己インダクタンス[H]
ここで、結合係数は0から1までの値のいずれかを取りますが、漏れ磁束がない理想的な条件において、k=1となります。つまり、( ウ )には「多く」が入り、( エ )には「![]() 」が入ります。
」が入ります。
最後の( オ )の部分で、和動接続とすると、合成インダクタンスはそれぞれの自己インダクタンス(L1、L2)に加えて、一方のコイル(コイル1)が他方(コイル2)のコイルの影響を受けて生じる相互インダクタンス(M)と、コイル2がコイル1の影響を受けて生じる相互インダクタンス(M)も加わるため、合計インダクタンスLwaは次の式のようになります。
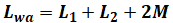
一方、これが差動接続の場合には、自己インダクタンスから相互インダクタンスを引くことになります。よって、この場合の合計インダクタンスLsaは次の式のようになります。
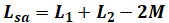
以上より、( オ )には「和動接続」が適切です。

コメント