問 題
三相誘導電動機があり、一次巻線抵抗が15[Ω]、一次側に換算した二次巻線抵抗が9[Ω]、滑りが0.1のとき、効率[%]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、励磁電流は無視できるものとし、損失は、一次巻線による銅損と二次巻線による銅損しか存在しないものとする。
- 75
- 77
- 79
- 82
- 85
正解 (2)
解 説
求めたいのは効率η[%]であり、それは、一次入力P1[W]と機械出力Pm[W]との比で表すことができます。一次入力P1[W]から一次銅損Pc1[W]を引いたものが二次入力P2[W]で、そこからさらに二次銅損Pc2[W]を引いたものが機械出力Pm[W]なので、要するに次のような式が成り立ちます。
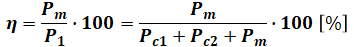
つまり、Pc1とPc2がそれぞれPmの何倍かを知ることが、この問を解く上での目的となります。
まず押さえておきたい知識として、二次銅損Pc2[W]の値は、二次入力P2[W]のs倍となります。よって、
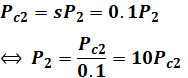
となり、また、上記の通り、二次入力P2[W]から二次銅損Pc2[W]を引いたものが機械出力Pm[W]なので、
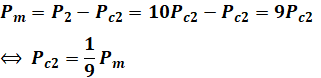
となります。
一方、一次銅損Pc1[W]と二次銅損Pc2[W]は比例関係にあり、その比は一次巻線抵抗r1[Ω]と二次巻線抵抗r2[Ω]の比になります。よって、次のような式が成り立ちます。
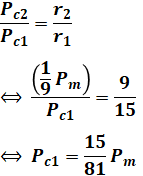
以上より、最初の式にこれらの計算結果を代入していくと、求めたい効率を計算することができます。
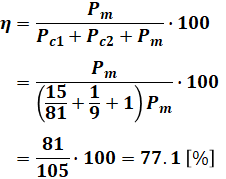

コメント