問 題
こう長20[km]の三相3線式2回線の送電線路がある。受電端で33[kV]、6600[kW]、力率0.9の三相負荷に供給する場合、受電端電力に対する送電損失を5[%]以下にするための電線の最小断面積[mm2]の値として、計算値が最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、使用電線は、断面積1[mm2]、長さ1[m]当たりの抵抗を1/35[Ω]とし、その他の条件は無視する。
- 14.3
- 23.4
- 24.7
- 42.8
- 171
正解 (4)
解 説
送電損失(線路損失)の計算式は以下のように表されます。
![]()
- Ploss:線路損失 [W]
- R:線路抵抗 [Ω]
- I:電流 [A]
ちなみに、係数の3は、3線分の合計という意味です。
また、このうち線路抵抗Rは線路の長さに比例し、線路の断面積に反比例するため、次のように書けます。
![]()
- ρ:抵抗率(断面積1mm2、長さ1m当たりの抵抗Ω) 1/35 [(Ω・mm2)/m]
- l:導体の長さ 20×103 [m]
- A:電線の断面積 [mm2]
一方、三相3線式の受電端電力と受電端電圧、力率がわかっているので、電流I[A]は次の通りとなります。ただし、問題文にある受電端電力6600[kW]というのは2回線分の電力なので、ここでは1回線分に換算しています。
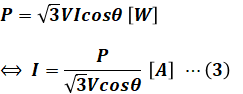
- P:1回線あたりの受電端電力 3300×103 [W]
- V:受電端電圧 33×103 [V]
- cosθ:力率 0.9
問われているのは、送電損失(線路損失)が受電端電力の5[%]になる電線の断面積A[mm2]を求めることです。
上記で示した線路損失Plossの式は1回線あたりの話なので、受電端電力も2回線分ではなく1回線あたりに換算すると、以下のように計算することができます。
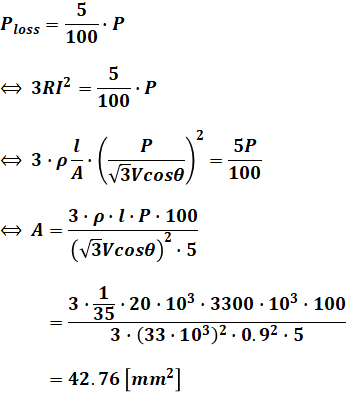
以上から、正解は(4)となります。

コメント