問 題
三相3線式1回線の専用配電線がある。変電所の送り出し電圧が6600V、末端にある負荷の端子電圧が6450V、力率が遅れの70%であるとき、次の(a)及び(b)の問に答えよ。
ただし、電線1線当たりの抵抗は0.45Ω/km、リアクタンスは0.35Ω/km、線路のこう長は5kmとする。
(a) この負荷に供給される電力P1の値[kW]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 180
- 200
- 220
- 240
- 260
(b) 負荷が遅れ力率80%、P2[kW]に変化したが線路損失は変わらなかった。P2の値[kW]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 254
- 274
- 294
- 314
- 334
解 説
(a)
まず、問題文で与えられた各数値をまとめると、下図のように表すことができます。抵抗とリアクタンスの値は[Ω/km]と[km]の掛け算で求めています。

ここで、求めたいのは負荷に供給される電力P1の値[kW]なので、下式の通りです。
![]()
- P1:電力 [W]
- Vr:受電端電圧 [V]
- I:電流 [A]
- cosθ:負荷の力率
(1)式より、P1を求めるためにはIの値を知る必要があります。上図に記載している各種の数値からIを求めるには、次に示す電圧降下の式を使うのが有効です。
![]()
- Vd:電圧降下 [V]
- Vs:送電端電圧 [V]
- Vr:受電端電圧 [V]
- I:線電流 [A]
- R:抵抗(電線1条あたり) [Ω]
- X:リアクタンス(電線1条あたり) [Ω]
- cosθ:負荷の力率
以下、(2)式に上図の値を代入してIで解きます。
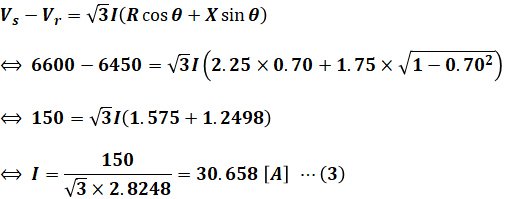
そして、(3)式を(1)式に代入することで、求めたいP1を算出することができます。
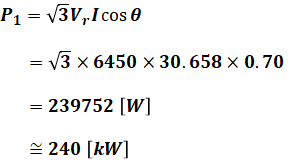
よって、正解は(4)です。
(b)
設問(b)も電力を求める問題なので、最終的に使う式は設問(a)の場合と同じ式です。
![]()
(4)式において、θ2は力率80%という条件から、θ2=0.80だとすぐに決まります。よって、Vr2とI2の値を求めるのが当面の目標となります。
まず、問題文に「線路損失は変わらなかった」と書かれているので、線路損失の式を使って考えてみることにします。
![]()
- Ploss:線路損失 [W]
- R:線路抵抗 [Ω]
- I:電流 [A]
(5)式が線路損失の公式ですが、これを見るとわかる通り、電流Iは線路損失Plossと線路抵抗Rで決まる値です。今回の場合、Plossが不変だと明記されていて、Rも設問(a)と同じ線路を使っているので変わりません。よって、Iの値は設問(a)・(b)のどちらでも同じ値となります。
![]()
これでI2の値がわかったので、次にVr2を求めます。設問(a)の(2)式をうまく利用すれば、以下のようにVr2を算出することができます。
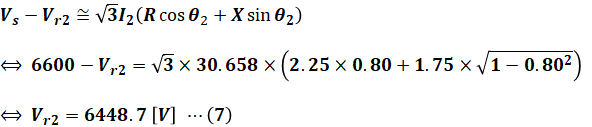
最後に、(6)式と(7)式の値を(4)式に代入すれば、求めたいP2を算出することができます。
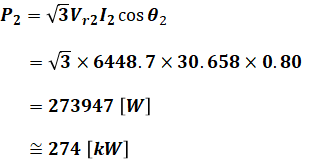

コメント