問 題
揚水発電所について、次の(a)及び(b)の問に答えよ。
ただし、水の密度を1000kg/m3、重力加速度を9.8m/s2とする。
(a) 揚程450m、ポンプ効率90%、電動機効率98%の揚水発電所がある。
揚水により揚程及び効率は変わらないものとして、下池から1800000m3の水を揚水するのに電動機が要する電力量の値[MW・h]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 1500
- 1750
- 2000
- 2250
- 2500
(b) この揚水発電所において、発電電動機が電動機入力300MWで揚水運転しているときの流量の値[m3/s]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 50.0
- 55.0
- 60.0
- 65.0
- 70.0
解 説
(a)
揚水を行うには、理論的には位置エネルギーの分だけ必要で、現実的にはそれに電動機効率とポンプ効率による損失分を加味することになります。
よって、揚水を行うのに消費するエネルギーは次のような計算式で表すことができます。
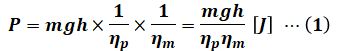
- P:揚水で使うエネルギー [J]
- m:水の質量 [kg]
- g:重力加速度 9.8[m/s2]
- h:高さ(揚程) [m]
- ηp:ポンプの総合効率
- ηm:電動機の総合効率
(1)式において、質量mは水の体積と密度を掛ければよいので、問題文で与えられた各数値を代入していくと、以下のように計算することができます。
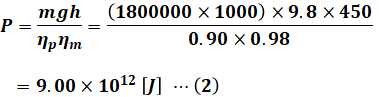
ここで、問われているのは電力量の値[MW・h]なので、(2)式の結果から単位を合わせていく必要があります。[J]=[W・s]、1[MW]=1×106[W]、1[h]=3600[s]より、(2)式は次の(3)式のようになります。
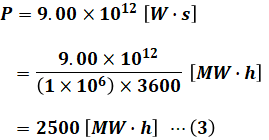
よって、正解は(5)です。
(b)
(b)でも(a)で用いた(1)式を使って計算することができるので、以下に(1)’式を示します。
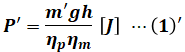
- P’:揚水で使うエネルギー [J]
- m’:水の質量 [kg]
- g:重力加速度 9.8[m/s2]
- h:高さ(揚程) [m]
- ηp:ポンプの総合効率
- ηm:電動機の総合効率
ここで問われているのは流量の値[m3/s]ですが、水の密度は問題文で与えられているので、「1秒あたり」に流れる水の質量mがわかれば答えを求めることができます。よって、今回は上式のPもmも1秒あたりの量について考えます。
つまり、エネルギーP’は1秒あたりのエネルギーと考えるので、単位が[J/s]=[W]となり、水の質量m’も1秒あたりとするので単位が[kg/s]となります。この条件で計算を進めると、次に示すように(1)’式からm’を算出できます。
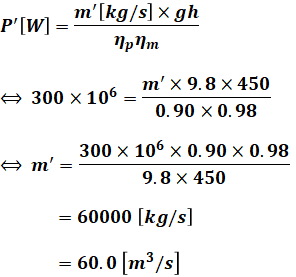
よって、正解は(3)となります。

コメント