問 題
定格容量が10kV・Aで、全負荷における銅損と鉄損の比が2:1の単相変圧器がある。力率1.0の全負荷における効率が97%であるとき、次の(a)及び(b)の問に答えよ。
ただし、定格容量とは出力側で見る値であり、鉄損と銅損以外の損失は全て無視するものとする。
(a) 全負荷における銅損は何[W]になるか、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 357
- 206
- 200
- 119
- 115
(b) 負荷の電圧と力率が一定のまま負荷を変化させた。このとき、変圧器の効率が最大となる負荷は全負荷の何[%]か、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 25.0
- 50.0
- 70.7
- 100
- 141
解 説
(a)
問題文より、定格容量が10[kV・A]で力率が1.0なので、出力Poutはそのまま10[kW]となります。よって、効率ηは問題文より97%なので、下式が成り立ちます。
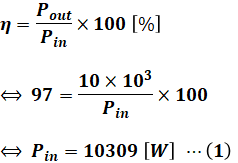
- η:効率
- Pin:入力 [W]
- Pout:出力 [W]
ここで、鉄損と銅損以外の損失は無視できるので、入力Pinから鉄損P鉄と銅損P銅の両方を引いたものが、出力Poutと一致します。
![]()
また、全負荷における銅損P銅と鉄損P鉄の比が2:1であることが問題文で与えられているので、これを式で表すと以下のようになります。
![]()
よって、(1)式と(3)式を(2)式に代入して銅損P銅について解けば、問われている銅損P銅を計算することができます。
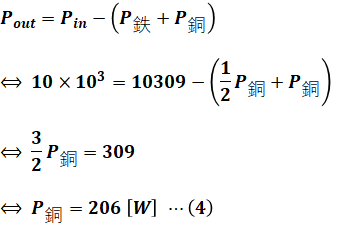
以上から、正解は(2)です。
(b)
変圧器の効率が最大となる負荷が問われていますが、最も効率が良くなるのは「鉄損=銅損」となるときです。これは式を使って証明することもできますが、結論だけを覚えておけば充分だと思うので、ここでは割愛します。
よって、変圧器の効率が最大となる条件では、鉄損P鉄と銅損P’銅の関係式は次のようになります。
![]()
上式において、鉄損P鉄は無負荷損ともいわれ、負荷電流が流れていてもいなくて関係なく生じる損失なので、ここでも設問(a)での全負荷のときと同じ値となります。つまり、(4)式で全負荷時の銅損が206[W]とわかっていて、鉄損は(3)式より銅損の半分なので、鉄損は次のように計算できます。
![]()
一方、銅損P’銅は負荷損ともいわれ、負荷電流が流れているときだけ生じる損失です。これは負荷率αの2乗に比例します。今回の場合、無負荷なら0[W]、全負荷なら設問(a)の(4)式より206[W]となります。
![]()
求めたいのは負荷率αなので、(7)式に(4)式、(5)式、(6)式を代入してαについて解けば、答えを求めることができます。
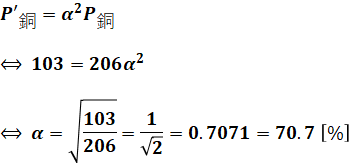
以上から、正解は(3)となります。

コメント