問 題
図は昇降圧チョッパを示している。スイッチQ、ダイオードD、リアクトルL、コンデンサCを用いて、図のような向きに定めた負荷抵抗Rの電圧v0を制御するためのものである。
これらの回路で、直流電源Eの電圧は一定とする。また、回路の時定数は、スイッチQの動作周期に対して十分に大きいものとする。
回路のスイッチQの通流率γとした場合、回路の定常状態での動作に関する記述として、誤っているものを次の(1)~(5)のうちから一つ選べ。
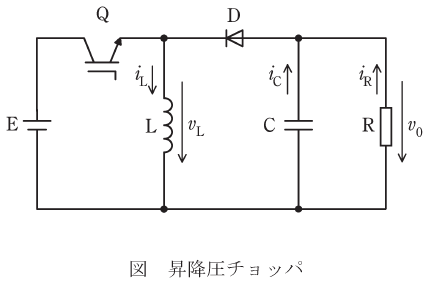
- Qがオンのときは、電源EからのエネルギーがLに蓄えられる。
- Qがオフのときは、Lに蓄えられたエネルギーが負荷抵抗RとコンデンサCにDを通して放出される。
- 出力電圧v0の平均値は、γが0.5より小さいときは昇圧チョッパ、0.5より大きいときは降圧チョッパとして動作する。
- 出力電圧v0の平均値は、図のv0の向きを考慮すると正になる。
- Lの電圧の平均電圧vLは、Qのスイッチング一周期で0となる。
解 説
(1)で、スイッチQがオンのときは、下図の赤矢印のように「E-Q-L」の経路と「C-R」の経路の二つで電流が流れます。
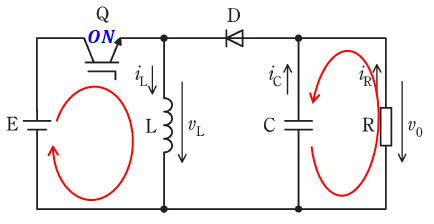
「E-Q-L」の経路(上図左側の赤矢印)では、電源EからのエネルギーがリアクトルLに蓄えられます。電流の向きは電源から考えると右回りとなることがわかります。
一方、「C-R」の経路(上図右側の赤矢印)では、コンデンサCに蓄えられていたエネルギーが負荷Rに放出されます。この時点で電流の向きを考えるのは難しいかもしれませんが、コンデンサが充電される向き(画面下から上)の反対(画面上から下)となります。充電時の向きの決め方は(2)の解説を参照してください。
よって、(1)は正しいです。
(2)で、スイッチQがオフのときは、下図の赤矢印のように「L-(CとRの並列回路)-D」の経路で電流が流れ、Lに蓄えられたエネルギーがCとRに向かって放出されます。
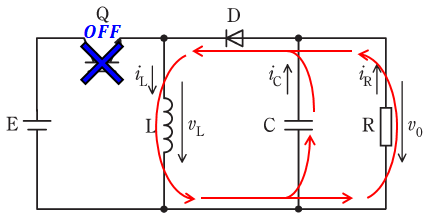
電流の向きはダイオードDに注目するとわかりやすいです。Dの向きから、ここでは画面右側から左側に電流が流れるので、Lでは下向きに、CとRでは上向きに電流が流れます。
よって、(2)は正しいです。
(3)について、通流率γとは、全体の時間Tのうちのスイッチオンの時間Tonの割合のことです。よって、下式のように表すことができます。
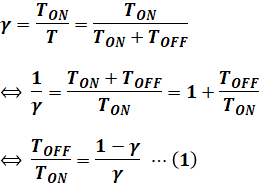
次に、選択肢(1)と(2)の解説で示した通り、リアクトルLはスイッチオンでエネルギーを溜めて、スイッチオフでそれを放出します。この際、溜める分と放出する分のエネルギーは等しいです。
エネルギー量は電圧と時間の積に比例するため、スイッチオン時とオフ時のそれぞれにおけるLの電圧と時間の積(これを電圧時間積といいます)の大きさは、等式で結ぶことができます。
ここで、スイッチオン時のLの電圧は、選択肢(1)の解説の図より、vL=-E[V]です。また、スイッチオフ時のLの電圧は、選択肢(2)の解説の図より、vL=v0[V]です。よって、電圧時間積の大きさが等しいので、次の等式が成り立ちます。
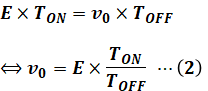
よって、(1)式を(2)式に代入すると、次のように計算できます。
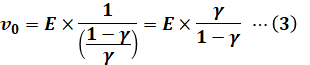
ここまで長かったですが、これでやっと選択肢(3)の内容を吟味する準備が整いました。
γが0.5より小さいときは、(3)式よりv0がEよりも小さくなります。たとえばγ=0.1として(3)式を計算すれば、v0=0.11Eです。よって、このときは降圧チョッパとして動作していることがわかります。
一方、γが0.5より大きいときは、(3)式よりv0がEよりも大きくなります。たとえばγ=0.9として(3)式を計算すれば、v0=9Eです。よって、このときは昇圧チョッパとして動作していることがわかります。
以上から、(3)の記述は反対になっているので、これが誤っていて正解の選択肢であると判断することができます。
(4)に関して、(1)と(2)の解説で示した図の通り、スイッチオン時でもオフ時でも電流iRは問題の図の通り下から上向きとなります。よって、出力電圧v0は上から下向きとなり、問題の図と一致しているため「正」と判断できます。そのため、(4)は正しいです。
(5)で、(3)の解説の通り、リアクトルLはスイッチオンでエネルギーを溜めて、スイッチオフでそれを放出します。溜める分と放出する分は等しいので、スイッチング1周期分の電圧の平均値はプラスとマイナスで相殺されて0になります。よって、(5)は正しいです。
以上から、正解は(3)となります。

コメント
本当に些細なツッコミで申し訳ないのですが(2)の解説の結論(1)ではなく(2)では
いえ、このようなミスは自分では気づきにくいので、とても助かります。
ご指摘ありがとうございます!