問 題
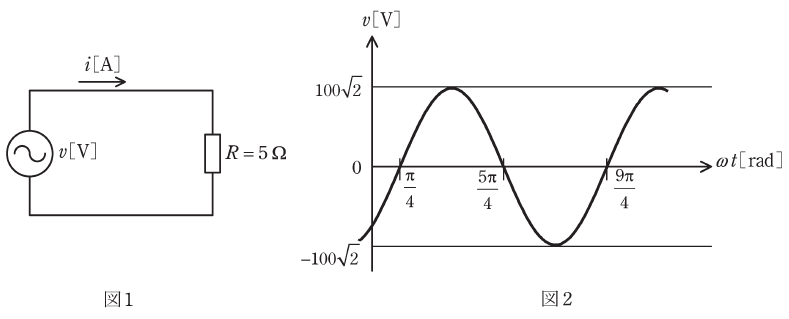
図1の回路において、図2のような波形の正弦波交流電圧v[V]を抵抗5Ωに加えたとき、回路を流れる電流の瞬時値i[A]を表す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、電源の周波数を50Hz、角周波数をω[rad/s]、時間をt[s]とする。
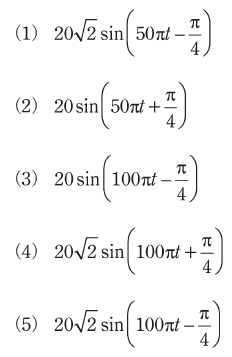
正解 (5)
解 説
交流回路での電流の瞬時値i[A]は、下式が基本構造となります。
![]()
- i:電流の瞬時値 [A]
- I:電流の実効値 [A]
- √2I:電流の最大値 [A]
- ω:各周波数 [rad/s]
- t:時間 [s]
- θ:位相(遅れ) [rad]
まずは電流Iについて考えます。電圧の最大値が図2より100√2[V]で、抵抗が5[Ω]なので、下式のように電流の最大値√2I[A]を使った等式ができ、Iの値が計算できます。
![]()
また、各周波数ωは、問題文に周波数f=50[Hz]とあることから、以下の計算によって求められます。
![]()
最後に位相θについて考えます。図2を見ると、縦軸に最も近い位置でv=0となるのが、ωt=π/4であることがわかります。よって、これは位相がπ/4だけ遅れていることになるので、θ=π/4となります。
以上で求めたI、ω、θを最初の式に代入すれば、求める答えが出ます。
![]()
よって、正解は(5)です。

コメント