問 題
次の文章は、平行板コンデンサに関する記述である。
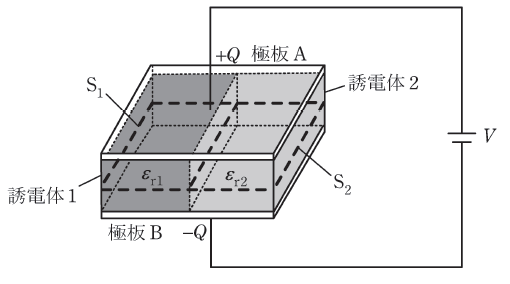
図のように、同じ寸法の直方体で誘電率の異なる二つの誘電体(比誘電率εr1の誘電体1と比誘電率εr2の誘電体2)が平行板コンデンサに充填されている。
極板間は一定の電圧V[V]に保たれ、極板Aと極板Bにはそれぞれ+Q[C]と-Q[C](Q>0)の電荷が蓄えられている。誘電体1と誘電体2は平面で接しており、その境界面は極板に対して垂直である。ただし、端効果は無視できるものとする。
この平行板コンデンサにおいて、極板A、Bに平行な誘電体1、誘電体2の断面をそれぞれ面S1、面S2(面S1と面S2の断面積は等しい)とすると、面S1を貫く電気力線の総数(任意の点の電気力線の密度は、その点での電界の大きさを表す)は、面S2を貫く電気力線の総数の( ア )倍である。
面S1を貫く電束の総数は面S2を貫く電束の総数の( イ )倍であり、面S1と面S2を貫く電束の数の総和は( ウ )である。
上記の記述中の空白箇所(ア)~(ウ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
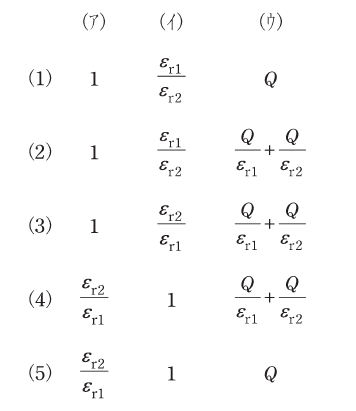
解 説
まず、問題の図を回路図に描き換えると、次のようになります。
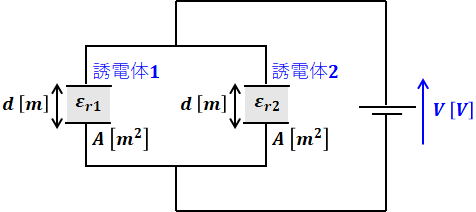
( ア )では電気力線の総数の比が問われていますが、問題文より「任意の点の電気力線の密度は、その点での電界の大きさを表す」(電気力線の密度=電界)とあるので、実質的に、電界E[V/m]に板の面積A[m2]を掛けたものが、電気力線の総数となります。
ここで、電界E[V/m]は次の式で求めることができます。これは重要公式として押さえておいてください。
![]()
- E:電界の強さ [V/m]
- V:電圧 [V]
- d:板間距離 [m]
上図の回路図を見てもわかる通り、今回は誘電体1のほうも誘電体2のほうも、ともに極板間の電圧はV[V]、距離はd[m]で同じです。ということは、電界の強さE[V/m]で同一となります。
また、板の面積A[m2]についても双方は同じ大きさであるため、結局、電気力線の総数(=電界×板の面積)についても、誘電体1側と誘電体2側で同じ数となります。
よって、( ア )では電気力線の総数の比を答えればよいので、ここには「1」が入ります。
( イ )では電束の総数の比が問われています。電束とは「1[C]分の電気力線のまとまり」のことなので、電束の総数の比を求めたいなら、電荷Q[C]の比を求めればよいです。
電荷Q[C]は次の式で求めることができます。
![]()
- Q:電荷[C]
- C:静電容量[F]
- V:電圧[V]
さらに、静電容量C[F]は次の式で求めることができます。
![]()
- ε:誘電率[F/m]
- A:板の面積[m2]
- d:板間距離[m]
よって、これらを組み合わせると、以下のようになります。
![]()
誘電体1側、誘電体2側の電荷QをそれぞれQ1、Q2とすると、その比Q1/Q2は次のように計算することができます。
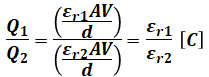
これが電束の総数の比になるので、( イ )には「εr1/εr2」が入ります。
( ウ )について、問題文や問題の図ですでに誘電体が充填された状態として、極板間にはQ[C]の電荷が蓄えられていることが名言されています。
面S1と面S2を貫く電束の数の総和というのは、極板間の電荷のことなので、何か計算をする必要もなくここはQ[C]となることがわかります。よって、( ウ )には「Q」が入ります。
以上から、( ア )には「1」が、( イ )には「εr1/εr2」が、( ウ )には「Q」が入るので、正解は(1)です。

コメント