問 題
こう長25kmの三相3線式2回線送電線路に、受電端電圧が22kV、遅れ力率0.9の三相平衡負荷5000kWが接続されている。次の(a)及び(b)の問に答えよ。ただし、送電線は2回線運用しており、与えられた条件以外は無視するものとする。
(a) 送電線1線当たりの電流の値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、送電線は単導体方式とする。
- 42.1
- 65.6
- 72.9
- 126.3
- 145.8
(b) 送電損失を三相平衡負荷に対し5%以下にするための送電線1線の最小断面積の値[mm2]として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、使用電線は、断面積1mm2、長さ1m当たりの抵抗を1/35Ωとする。
- 31
- 46
- 74
- 92
- 183
解 説
(a)
問題文にある三相3線式2回線送電線路の等価回路を図示すると、次のように表すことができます。
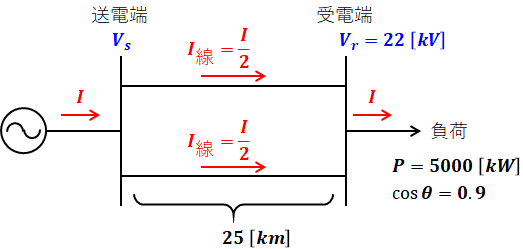
求めたいのは送電線1線当たりの電流の値ですが、考えやすそうなのは多くのパラメータが集まっている負荷のところです。負荷に注目すると、電力Pや電圧Vr、力率cosθがわかっているので、三相回路の電力を求める公式を使えば、負荷を流れる電流Iを求めることができます。
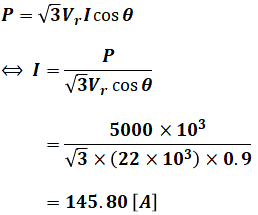
ただし、これは負荷を流れる電流Iであり、送電線1線当たりの電流I線ではありません。上図の等価回路を見てもわかるように、送電線1線当たりの電流I線は負荷電流Iの半分となります。
![]()
よって、正解は(3)です。
(b)
送電損失を負荷電力Pの5%以下に抑えたいという話なので、まずは送電損失の式を確認しておきます。
三相3線式送電線路の送電損失(線路損失)の計算式は、「一般的には」以下のように表されます。
![]()
- Ploss:線路損失[W]
- R:線路抵抗[Ω]
- I:電流[A]
上式の係数の3は、3線分の合計という意味です。
これは重要公式として押さえておくべき式ですが、今回はここで注意が必要です。上式は一般的な「三相3線式1回線送電線」の話であり、今回のような「三相3線式2回線送電線路」の場合は、回線が倍になるので損失Ploss(2)もこの倍になります。
また、電流Iは送電線を流れる電流なので、設問(a)の解説を踏まえると、これは電流I線のことです。
![]()
上式のうち線路抵抗Rは、線路の長さに比例し、線路の断面積に反比例するため、次のように書けます。
![]()
- ρ:抵抗率(断面積1mm2、長さ1m当たりの抵抗Ω) [(Ω・mm2)/m]
- l:導体の長さ [m]
- A:電線の断面積 [mm2]
(2)式を(1)式に代入すると(3)式のようになります。
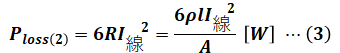
求めたいのは、送電損失(線路損失)が負荷電力5000[kW]の5%になるときの電線の断面積A[mm2]の値です。よって、次のように等式を解くことで、Aを求めます。
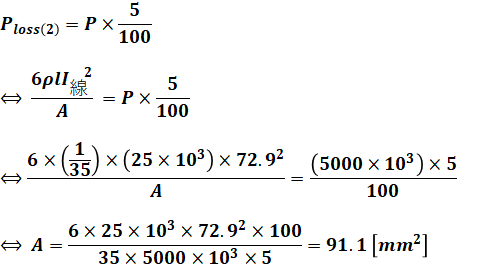
以上から、選択肢の中で最も近いのが(4)の「92」となるため、正解は(4)です。

コメント