電験三種 R2年 理論 問1 問題と解説

　問 題　　　　　

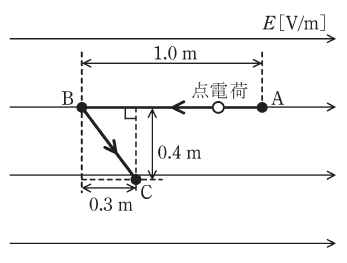
図のように、紙面に平行な平面内の平等電界E[V/m]中で2Cの点電荷を点Aから点Bまで移動させ、さらに点Bから点Cまで移動させた。この移動に、外力による仕事W＝14Jを要した。

点Aの電位に対する点Bの電位V_BA[V]の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、点電荷の移動はゆっくりであり、点電荷の移動によってこの平等電界は乱れないものとする。

1. 5
2. 7
3. 10
4. 14
5. 20

 

 

 

 

 

　解 説　　　　

求めたいのは点A－点B間の電位差V_BA[V]ですが、これは問題文に記載されている単位からもわかる通り、E[V/m]と距離d[m]との積となります(dは問題の図より1.0[m]です)。

上式よりEを求めるのが当面の目標となりますが、点A → 点Cの仕事W[J]が与えられているため、ここから考えます。ちなみに、実際には点A → 点B → 点Cと移動していますが、仕事W[J]は最初と最後だけで決まり、その過程にどのような道をたどっていても関係ないので、点Bは気にしなくて大丈夫です。

仕事W[J]は力F[N]と距離d'[m]で表すことができます。さらに、力F[N]は電荷q[C]と電界E[V/m]との積で表すことができるので、これらを式にすると次のようになります。

ここで問題文を見ると、(2)式のうち、W＝14[J]、q＝2[C]であることがわかり、d’はAC間の距離となります(前述の通り、点Bは無視してAC間に注目します)。

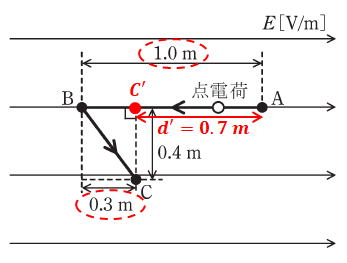
ただし、この距離というのは、電界の中での距離であることに注意してください。つまり、AC間を線で結んで三平方の定理…などと考えるのではなく、下図のように点Cを電界と平行に移動させた点C’を考えて、その上で点Aと点C’の距離を求めます。

以上でわかった値を(2)式に代入すると、E[V/m]を算出することができます。

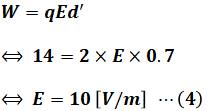
さらに(4)式を(1)式に代入すると、問われているV_BA[V]を求めることができます。

よって、正解は(3)です。