問 題
かごの質量が250kg、定格積載質量が1500kgのロープ式エレベータにおいて、釣合いおもりの質量は、かごの質量に定格積載質量の50%を加えた値とした。
このエレベータの電動機出力を22kWとした場合、一定速度でかごが上昇しているときの速度の値[m/min]はいくらになるか、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、エレベータの機械効率は70%、積載量は定格積載質量とし、ロープの質量は無視するものとする。
- 54
- 94
- 126
- 180
- 377
解 説
エレベータの昇降に使用する電動機の出力P[W]は次の式で求めることができます。この式は重要ですので、ぜひ押さえておいてください(といっても、位置エネルギーの考え方を使えば難しくはないと思います)。
![]()
- P:電動機の出力 [W]
- M:実質の質量 [kg] (M=MC+ML-MB)
- g:重力加速度 9.8 [m/s2]
- v:昇降速度 [m/min]
- η:機械効率 [%]
位置エネルギーの単位は[J]ですが、ここではMghのhに相当する部分が「高さ」ではなく、「速度(時間あたりに移動する高さ)」になっています。そのため、単位の[J]も[J/s]に変わるので、つまり、出力の単位である[W]になります。
また、昇降速度は問題文では分速として扱うことが多いですが、計算の際には秒速に直す(60で割る)必要があるので注意してください。そして、電動機の効率は100%ではなく、どうしてもある程度の損失が出てしまうので、上式の最後に機械効率ηで割っています。
以上を踏まえて、問題文で与えられた数値を上式に代入すれば求めたい昇降速度vは出るのですが、質量Mをいくつにするかは少し考えなければいけません。そのために、以下のような、電動機によるエレベータの昇降を図示したものを見てください。
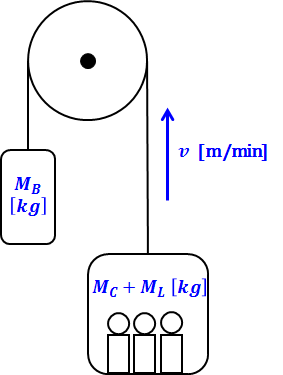
上図において、右下の四角形はエレベータのかごを示していて、かご質量はMCです。その中にいる人(または荷物)が描かれていますが、積載質量をMLで表しています。また、左にある四角形は釣り合いおもりと呼ばれるもので、この質量をMBとします。
エレベータを上昇させようとする際、そのままかごを持ち上げようとするとMC+MLを重力に逆らって上げなければいけませんが、釣り合いおもりがある場合、MBの重力の分だけ、かごを持ち上げる電動機の出力が小さくて済むようになっています。
このようにして、電動機の必要トルクを小さくすることで、エレベータの昇降を効率的に行うことができます。今回の場合は、MC=250kg、ML=1500kgであり、MBは問題文の条件より、
![]()
となります。よって、実質の質量Mは、
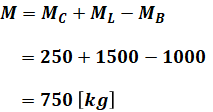
です。これを最初に示した公式に代入すると、求める答えが得られます。
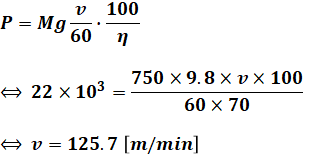
以上から、正解は(3)となります。

コメント