演算増幅器の計算例

増幅演算機の基本的な仕組みや回路図については前項で扱ったので、この項では、具体的な計算問題の解き方を紹介します。

例題

理想的な演算増幅器を用いた以下の回路があるとき、入力電圧V₁[V]に対する出力電圧V₂[V]の比の値はいくつになるでしょうか。

解説

この問題では「V₂/V₁」の値が問われているので、(回路全体の)増幅度を答える問題です。

演算増幅器が理想的であるということは、入力インピーダンスと(増幅器自体の)増幅度が∞で、出力インピーダンスは0です。入力インピーダンスが∞であれば、入力端子に電流が流れず、演算増幅器の2つの入力端子(+と-)の電圧は等しくなります。

よって、以下の図の青字のV₁[V]のように書けます。

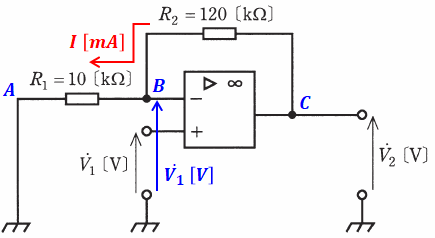
また、上図に青字で記入しているように、R₁とR₂を流れる電流はどちらも同じ大きさI[mA]です。これは、入力インピーダンスが∞であり、演算増幅器側には電流が流れ込まないため、R₁を流れる電流がそのまま全てR₂へと流れるからです。

ちなみに、電流の単位を[A]ではなく[mA]としているのは、このあとの計算の都合上です。つまり、問題の図ではR₁やR₂の単位が[kΩ]になっているので、電流の単位を[mA]にしておくとオームの法則がそのまま使えて便利というだけの話です。ここで電流の単位を[A]にしても構いませんが、その場合は、R₁やR₂を10000[Ω]や120000[Ω]に直す必要が生じます。

上図において、Aの位置は接地されているので0[V]で、Bの位置はV₁[V]です。その間に10[kΩ]の抵抗R₁があり、そこをI[mA]の電流が流れていることから、オームの法則を適用すると、

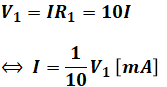
のようにV₁とIの関係式を求めることができます。

また、Bの位置から抵抗R₂を通ってCの位置へといく部分も以下のようにオームの法則で式を立てることができるので、先ほど求めたV₁とIの関係式を合わせて考えると、

のように計算することができ、求める増幅度(V₂/V₁)がわかります。

ちなみに、今回は問われているのが増幅度ですが、もし電圧利得を答える問題であれば、電圧利得の公式に当てはめて、

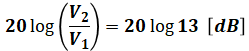
とすればよいだけで、その計算過程は増幅度の求め方と全く同様です。

また、log₁₀13=1.114などの対数の近似値(ほかにも、log₁₀2=0.301、log₁₀3=0.477など)については、問題を解くのに必要な情報は問題文で与えられるので、一つ一つ暗記する必要はありません。