問 題
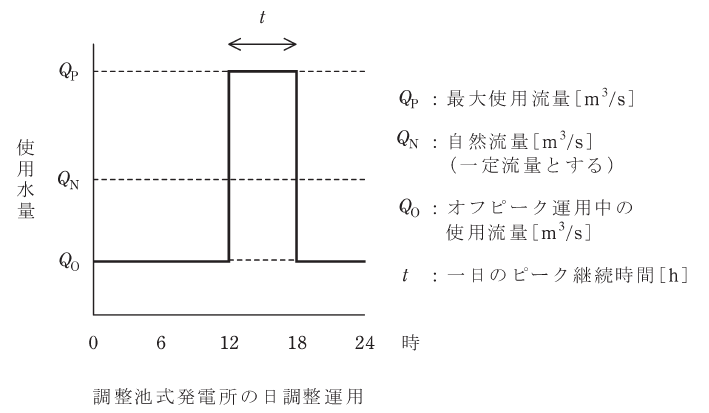
調整池の有効貯水量V[m3]、最大使用水量10m3/sであって、発電機1台を有する調整池式発電所がある。
図のように、河川から調整池に取水する自然流量QNは6m3/sで一日中一定とする。この条件で、最大使用水量QP=10m3/sで6時間運用(ピーク運用)し、それ以外の時間は自然流量より低い一定流量で運用(オフピーク運用)して、一日の自然流量分を全て発電運用に使用するものとする。
ここで、この発電所の一日の運用中の使用水量を変化させても、水車の有効落差、水車効率、発電機効率は変わらず、それぞれ100m、90%、96%で一定とする。
この条件において、次の(a)及び(b)の問に答えよ。
(a) このときの運用に最低限必要な有効貯水量V[m3]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 86200
- 86400
- 86600
- 86800
- 87000
(b) オフピーク運用中の発電機出力[kW]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 2000
- 2500
- 3000
- 3500
- 4000
解 説
(a)
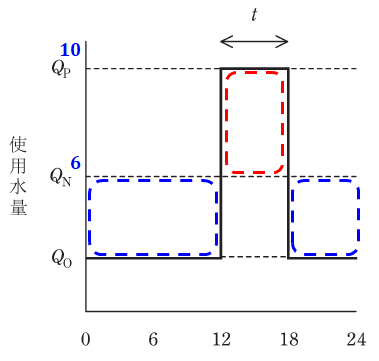
上図において、青点線部分が水の溜まっていく時間帯で、赤点線部分が溜まった水を使っていく時間帯です。つまり、貯水量は12時の時点で最も多く、18時の時点が最も少ないです。
(a)では最低限の水量が問われているので、18時の時点では少ないどころか空であると仮定します。よって、赤点線で囲った面積が、運用に最低限必要な有効貯水量Vとなります。
ただし、図の縦軸の単位は[m3/s]、横軸の単位は[h]なので、時間の単位が合っていません。よって、これをそろえる必要があります。[s]に合わせても[h]に合わせても構いませんが、以下の式では[s]に合わせています。
![]()
よって、正解は(2)です。
(b)
水力発電の出力は以下の式で表すことができます。
![]()
- P:発電機出力[kW]
- Q:流量[m3/s]
- H:有効落差[m]
- ηt:水車効率
- ηg:発電機効率
この問題ではオフピーク運用中の出力を問われているので、Q=QOで、そのほかのH、ηt、ηgはすでに問題文で数値が与えられています。よって、QOを求めるのがこの問題の最大のポイントです。
(a)の解説で示した図を再び見ると、青点線部分が水の溜まっていく時間帯で、赤点線部分が溜まった水を使っていく時間帯です。問題文に「一日の自然流量分を全て発電運用に使用する」とあるので、溜まった分は全て使い切ると考えると、赤点線の面積(消費)と青点線の面積(貯水)は同じになります。
よって、以下の等式(左辺が赤色、右辺が青色)が成り立ち、これを解くとQOを求めることができます。
※ ここでは水量そのものを求めるのではなく両辺を比較したいだけなので、わざわざ時間を秒に変換していません。が、もちろん直してから計算しても構いません。
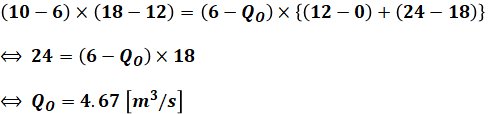
以上から、発電機出力Pは以下のように計算できます。
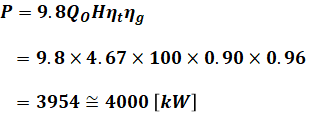
よって、正解は(5)です。

コメント