問 題
空気(比誘電率1)で満たされた極板間距離5d[m]の平行板コンデンサがある。図のように、一方の極板と大地との間に電圧V0[V]の直流電源を接続し、極板と同形同面積で厚さ4d[m]の固体誘電体(比誘電率4)を極板と接するように挿入し、他方の極板を接地した。次の(a)及び(b)の問に答えよ。
ただし、コンデンサの端効果は無視できるものとする。
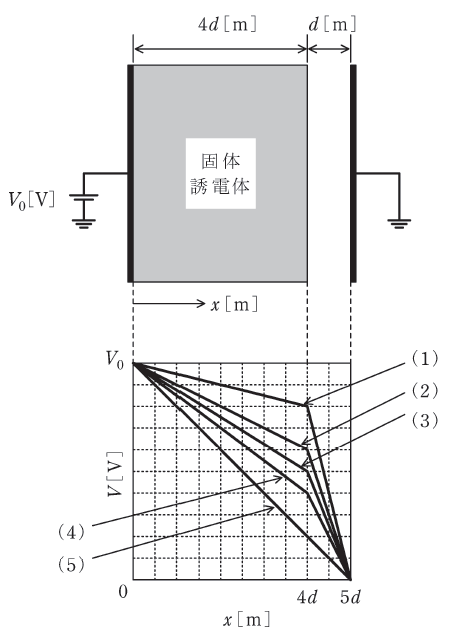
(a) 極板間の電位分布を表すグラフ(縦軸:電位V[V]、横軸:電源が接続された極板からの距離x[m])として、最も近いものを図中の(1)~(5)のうちから一つ選べ。
(b) V0=10kV、d=1mmとし、比誘電率4の固体誘電体を比誘電率εrの固体誘電体に差し替え、空気ギャップの電界の強さが2.5kV/mmとなったとき、εrの値として最も近いものを次の(1)~(5)のうちから一つ選べ。
- 0.75
- 1.00
- 1.3
- 1.67
- 2.00
解 説
(a)
ここでは、平行板コンデンサ間の電圧V0に対して、固体誘電体と空気ギャップ部分の電圧の内訳がポイントとなります。それを知るためには、以下に示す静電容量Cの式から考えると解きやすいと思います。
![]()
- C:静電容量[F]
- ε:誘電率[F/m]
- A:板の面積[m2]
- d:板間距離[m]
固体誘電体側の静電容量をC誘、空気ギャップ側の静電容量をC空とすると、それらの値は以下のように表すことができます。
![]()
![]()
以上の式からわかる通り、これらは同じ静電容量を持ちます。よって、電圧の内訳も等しくなるため、問題文のグラフにおいて、4dのところが0.5V0になっている(3)が正解となります。
ちなみに、ここではちょうど同じ静電容量だったので電圧の内訳を暗算で計算しましたが、固体誘電体にかかる電圧V誘と空気ギャップにかかる電圧V空をより正確に表現するなら、以下のように表します。
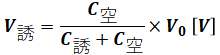
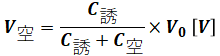 または
または ![]()
上式を使って計算しても、もちろんV誘=V空=0.5V0となります。
(b)
電界の強さと距離がわかっていれば、電圧を計算することができます。よって、問題文で与えられた条件を使うと空気ギャップにかかる電圧V’空が算出できます。
![]()
- V:電圧[V]
- d:板間距離[m]
- E:電界の強さ[V/m]
![]()
ここで、(a)の解説で紹介した式を使うと、以下のようにεrの値を含んだ方程式を立てることができるので、これを解けばεrを導出できます。
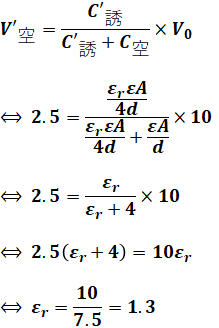

コメント