ブリッジ回路(ホイートストンブリッジ)

特徴的な電気回路に、ブリッジ回路と呼ばれる以下のような形の回路があります。

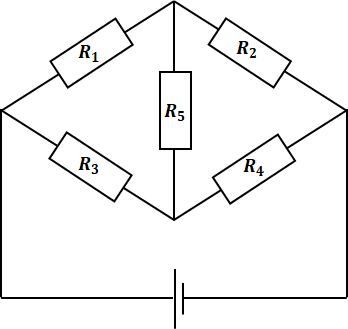
この回路には5つの抵抗が描かれていますが、そのうち真ん中の抵抗(R₅)に電流が流れないとき、このブリッジ回路は「平衡状態にある」と表現されます。平衡状態にあるときには、真ん中以外の4つの抵抗のうち、2組の対角線上の抵抗の積が等しくなります。

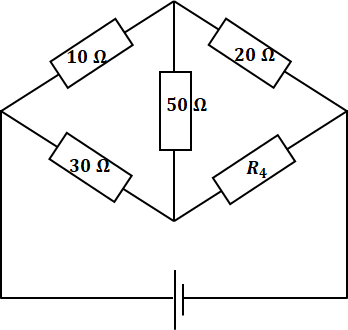
たとえば、以下のようにR₁～R₃とR₅が既知でR₄が未知の場合に、キルヒホッフの法則や鳳・テブナンの定理を使って複雑な式を解かなくても、この法則で簡単にR₄の値を求めることができます。

このルールはホイートストンブリッジの原理などとも呼ばれます(名称を覚える必要は特にありませんが)。

「平衡状態にあるときは」この原理が使えるといいながら、この形の回路が電験三種の試験で出題された場合、ほとんどのケースで平衡状態となっているはずなので、この回路図を見たら上記の式を思い出せるようにしておいてください。

また、上記では直流回路で表記していますが、ホイートストンブリッジの原理は交流回路においても成り立ちます。その場合、抵抗RではなくインピーダンスZとなるので、等式は次式で表現されます。

等式は直流のときと同様ですが、計算については複素数が入ってくる分、やや難しく(面倒に)なる点に注意してください。

ちなみに、上図はわかりやすいブリッジ回路ですが、以下のような回路図も同様にブリッジ回路となるので確認してください。見た目はちょっと違いますが、回路の構成としては上記と全く同じです。

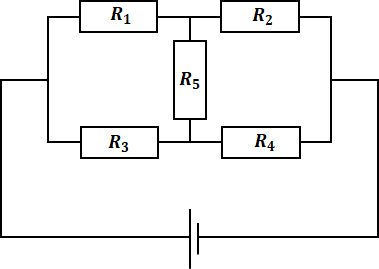
最後に、「平衡状態なのでR₅に電流が流れない」→「R₁×R₄=R₂×R₃が成り立つ」は正しい一方で、反対に「R₁×R₄=R₂×R₃が成り立つ」→「平衡状態となりR₅に電流が流れない」も正しいです。こちらの考え方からアプローチしていく必要がある問題もあります。