電験三種 H28年 機械 問16 問題と解説

　問題　　　　　

純抵抗を負荷とした単相サイリスタ全波整流回路の動作について、次の(a)及び(b)の問に答えよ。

(a)　図1に単相サイリスタ全波整流回路を示す。サイリスタT₁～T₄に制御遅れ角で、ゲート信号を与えて運転しようとしている。

T₂及びT₃のゲート信号は正しく与えられたが、T₁及びT₄のゲート信号が全く与えられなかった場合の出力電圧波形をe_d1とし、正しくT₁～T₄にゲート信号が与えられた場合の出力電圧波形をe_d2とする。

図2の波形1～波形3から、e_d1とe_d2の組合せとして正しいものを次の(1)～(5)のうちから一つ選べ。

　電圧波形e_d1電圧波形e_d2

(b)　単相交流電源電圧v_sの実効値をV[V]とする。ゲート信号が正しく与えられた場合の出力電圧波形e_d2について、制御遅れ角α[rad]と出力電圧の平均値E_d[V]との関係を表す式として、正しいものに最も近いものを次の(1)～(5)のうちから一つ選べ。

正解 (a)-(5), (b)-(2)

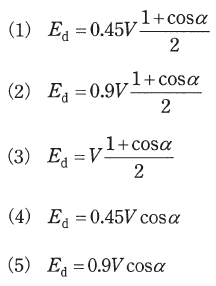
　解説　　　　

一部のゲート信号が機能しなかったときのe_d1と全てのゲート信号が与えられたときのe_d2が問われていますが、後者のほうが健全な状態なので、まずはこちらの考え方をしっかり押さえておきたいです。

T₁～T₄の全てのゲート信号が与えられた場合の電流の流れは、以下の図のようになります。

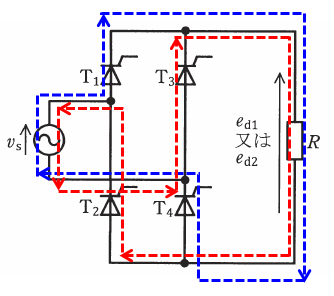
問題文の図2の一番上のグラフにおいて、「0～π」の範囲ではv_sが正になっています。上図ではv_sの矢印の向きと青点線の矢印の向きが一致しているため、つまり「0～π」の範囲では、T₁とT₄が関わっていることがわかります。

一方、図2のグラフで、「π～2π」の範囲はv_sが負になっていますが、上図におけるv_sの矢印の向きと赤点線の矢印が反対方向であることから、この範囲ではT₂とT₃が関わっていることがわかります。

今回は制御遅れ角α=π/2なので、「0～π/2」や「π～3π/2」の範囲ではe_dは0となり、上記の通り、それ以外の範囲では青点線と赤点線の電流が入れ替わるように流れるので、全てのゲート信号が与えられたときのe_d2の波形は、波形2のようになります。

そして、もしT₁とT₄が使えなかった場合、青点線の電流が流れなくなるので、上記の通り「0～π」の範囲でe_d1が0となります。

よって、このときの波形は波形3が適切であると判断できます。

以上より、(5)が正しいことがわかります。

この問題は問題文にもあるように、単相全波整流回路の問題だということをまず押さえておいてください。そして、(a)で考えてきたことはその瞬間ごとの出力電圧e_dを図示したものでしたが、実際に大事になってくるのは一瞬の電圧ではなく、全体で考えた際の平均電圧E_dです。

平均電圧E_dは、単相全波整流回路においては次式で表すことができます(Vは電源電圧v_sの最大値)。

これは重要なので公式として覚えてしまってよいと思いますが、もし計算をして出す場合は、以下のように導出できます。考え方としては、図2の波形2が描く面積を求めて、横軸の長さで割ることで、縦軸(e_d)の平均値を求めることができます。

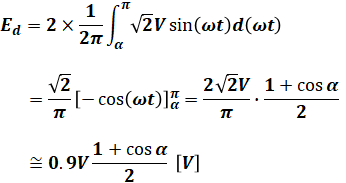
また、余談ですが、これが単相全波整流回路ではなく単相半波整流回路の場合、平均電圧E_dも全波のときの半分となるので、次のように表すことができます。こちらが出題されることがあるかもしれないので、併せて押さえておいてください。

電験三種 H28年機械問16 問題と解説