電験三種 H28年 理論 問9 問題と解説

　問 題　　　　　

図のように、R=1Ωの抵抗、インダクタンスL₁=0.4mH、L₂=0.2mHのコイル、及び静電容量C=8μFのコンデンサからなる直並列回路がある。

この回路に交流電圧V=100Vを加えたとき、回路のインピーダンスが極めて小さくなる直列共振角周波数ω₁の値[rad/s]及び回路のインピーダンスが極めて大きくなる並列共振角周波数ω₂の値[rad/s]の組合せとして、最も近いものを次の(1)～(5)のうちから一つ選べ。

　　　　ω₁ω₂

1. 2.5×10⁴3.5×10³
2. 2.5×10⁴3.1×10⁴
3. 3.5×10³2.5×10⁴
4. 3.1×10⁴3.5×10³
5. 3.1×10⁴2.5×10⁴

 

 

 

 

 

　解 説　　　　

問題文の図は抵抗とコイル2つとコンデンサがありますが、まずはこれらを合成したインピーダンスを式にします。先に並列に並んだコンデンサとコイルの合成インピーダンスZ_CL2について考えると、

と計算できるので、回路全体のインピーダンスZは次のように書くことができます。

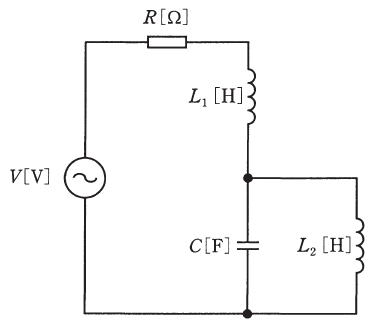
ここで、求めたいのは直列共振角周波数ω₁(Zが最小)と並列共振角周波数ω₂(Zが最大)の2つです。

Zを最小にするには、上式の虚部を0にすればよいです(ωを変えても実部は不変であるため)。よって、次のような計算を行うことによって、ω₁を求めることができます(以下の計算過程は一例です。ほかの解き方や、先に数値を代入しても構いません)。

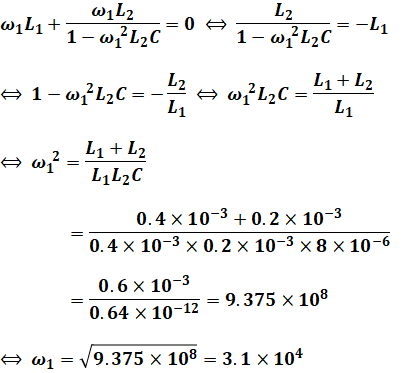
また、Zを最大にするには、先ほどの式のうち、第3項の分母が0になるようにすれば、Zは計算上無限大となるので極めて大きくなります。よって、次のような計算を行うことによって、ω₂を求めることができます。

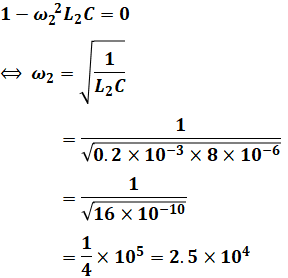
ちなみに、並列共振角周波数は並列に並んでいるコイルとコンデンサのリアクタンスが等しい(ωL=1/ωC)ときのωであるというのは重要事項なので、この式から解くこともできます。この考え方でも意味合いは上記のことと同じことなので、計算過程も同様となります。