問 題
図のように、内部抵抗r=0.1Ω、起電力E=9Vの電池4個を並列に接続した電源に抵抗R=0.5Ωの負荷を接続した回路がある。この回路において、抵抗R=0.5Ωで消費される電力の値[W]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
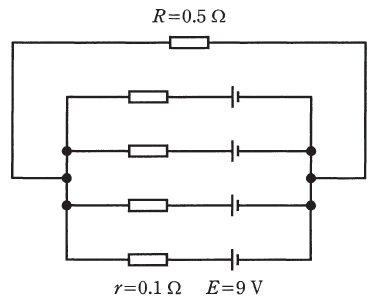
- 50
- 147
- 253
- 820
- 4050
解 説
この問題の回路は複雑ですが、求めたいのは抵抗Rで消費される電力の値なので、Rを流れる電流Iの大きさを求めればよいということになります。
このように、複雑な回路における「ある1つの抵抗」での電流または電圧だけを知りたいのであれば、「鳳・テブナンの定理」を用いるのが有効です。
鳳・テブナンの定理を用いれば、どんなに複雑な回路でも、以下の図のようにターゲットとしている抵抗以外の部分を1つの抵抗と1つの電源に置き換えることができます。

よって、上図右側におけるV’とr’を求めることが当面の目的となります。
鳳・テブナンの定理を使うにあたっては、まず初めに、目的の抵抗(今回は抵抗R)の両端で断線させて、これを含まない側の回路について考えます。つまり、以下のような回路からスタートします。
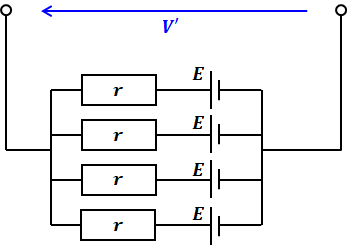
上図において、断線させた両端の電圧差が求めたいV’に相当します。上図の回路において、rに流れる電流が0なので、V’=E=9[V]となります。もし断線によってrに電流が流れなくなるということが感覚的に納得できない場合は、rに流れる電流をI’として考えてください。
4つのrは等価な環境にあるため、1つのrに流れる電流がI’であれば、ほかのrに流れる電流の大きさも向きも一緒のはずです。しかし、それでは4つのrの合流地点に流れる電流は4I’になるはずですが、その先は断線しているため、電流が流れる余地はありません。
よって、4I’=0 ⇔ I’=0となり、結局、rの両端の電位差は0なので、V’=Eとなります。
上記でV’がわかったので、続いてr’を求めます。r’を求めるには、上図において電源となる部分(今回は4つのE)を全て無いものと考えて(つまり短絡させて)、残った抵抗で計算した合成抵抗の値がr’に相当します。
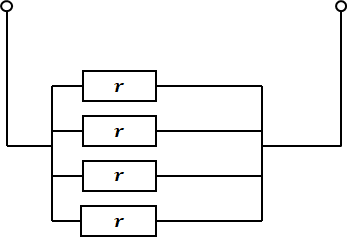
この問題では上図のように4つの等価な抵抗rが並行に並ぶので、その合成抵抗r’は、
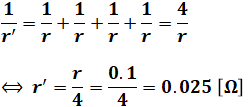
となります。
以上から、鳳・テブナンの定理を適用したあとの回路は次のようにまとめることができます。
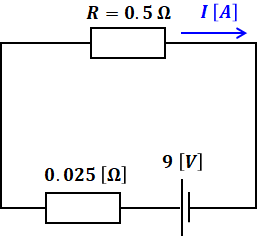
よって、Rを流れる電流Iは
![]()
となるので、Rで消費される電力Pは、次のように計算することができます。
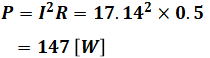

コメント