問 題
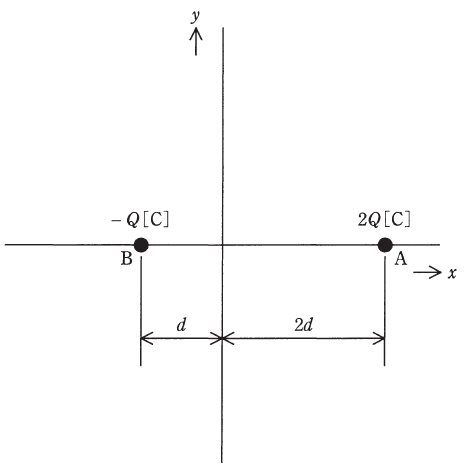
真空中において、図のようにx軸上で、距離3d[m]隔てた点A(2d,0)、点B(-d,0)にそれぞれ2Q[C]、-Q[C]の点電荷が置かれている。xy平面上で、電位が0Vとなる等電位線を表す図として、最も近いものを次の(1)~(5)のうちから一つ選べ。

解 説
点A、点Bに置かれている点電荷は、大きさが2:1で、符号は反対です。ということは、電位が0Vとなる点をCとすると、AのほうがBよりも電荷が大きいことから、これらを均衡に保つにはCからAまでの距離を、Bまでの距離の倍とらなくてはなりません。
つまり、AC:BC=2:1が成り立ちます。よって、わかりやすいところでいえば、直線AB上で、2:1となるような内分点と外分点は、どちらも点Cとしてふさわしいです。
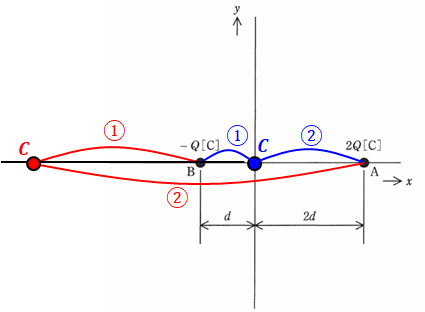
選択肢を見ると、内分点に関しては(1)~(5)のいずれもが満たしていますが、外分点を通っているのは(4)と(5)の2つだけです。ただし、(5)については直線AB上に2:1の内分点でも外分点でもない点(点Aの右側)があるので、これはおかしいです。
よって、正解は(4)に限られ、実際、(4)に示された軌跡は、直線AB上以外のどの部分についても、Aまでの距離とBまでの距離が2:1になっていることが読み取れます。
以上でこの問題を解くことはできましたが、選択肢から考えるのではなく、計算式から点Cの軌跡を導き出すこともできます。
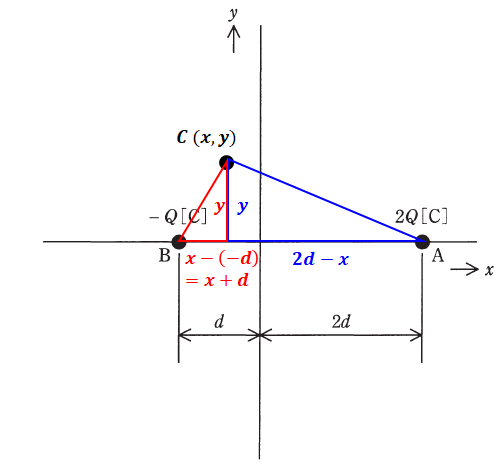
下図のように点Cの座標を(x,y)とすると、三平方の定理を使えば線分ACと線分BCの長さがわかります。そして、これらの長さの比が2:1になるような(x,y)を満たす軌跡が、求める点Cの軌跡となります。
![]()
![]()
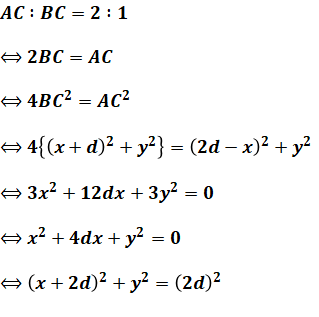
以上より、この軌跡は、中心が(-2d,0)で半径が2dの円だとわかるので、(4)が正解となります。

コメント