電験三種 H27年 電力 問16 問題と解説

　問 題　　　　　

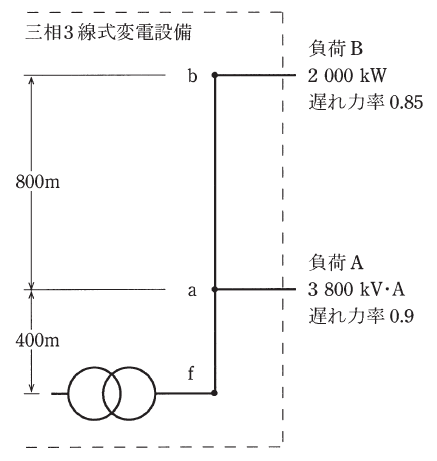
図は、三相3線式変電設備を単線図で表したものである。

現在、この変電設備は、a点から3800kV・A、遅れ力率0.9の負荷Aと、b点から2000kW、遅れ力率0.85の負荷Bに電力を供給している。b点の線間電圧の測定値が22000Vであるとき、次の(a)及び(b)の問に答えよ。

なお、f点とa点の間は400m、a点とb点の間は800mで、電線1条当たりの抵抗とリアクタンスは1km当たり0.24Ωと0.18Ωとする。また、負荷は平衡三相負荷とする。

(a)　負荷Aと負荷Bで消費される無効電力の合計値[kvar]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 2710
2. 2900
3. 3080
4. 4880
5. 5120

(b)　f-b間の線間電圧の電圧降下V_fbの値[V]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、送電端電圧と受電端電圧との相差角が小さいとして得られる近似式を用いて解答すること。

1. 23
2. 33
3. 59
4. 81
5. 101

 

 

 

 

 

　解 説　　　　

(a)

負荷Aは皮相電力3800kV・Aで遅れ力率0.9なので、無効電力Q_Aは次のように計算できます。

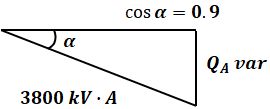
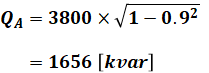
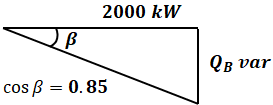
一方、負荷Bは有効電力2000kWで遅れ力率0.85なので、無効電力Q_Bは次のように計算できます。

負荷Aのときは皮相電力(直角三角形の斜辺)が既知でしたが、負荷Bでは有効電力(直角三角形の横)が既知であることに注意です。これらは単位から区別することができます(皮相→V・A、有効→W、無効→var)。

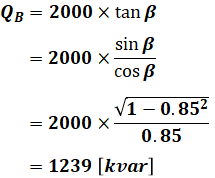
よって、無効電力の合計値は、

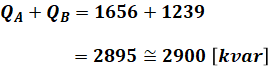
となります。

(b)

(b)を解くために、まず、問題文の図を以下のように描き替えます。

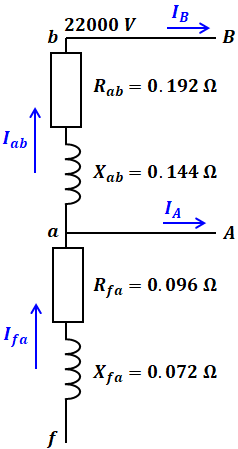
問題文の図では電線がまっすぐ表示されていますが、電線には抵抗とリアクタンスが1条あたりそれぞれ0.24Ω/km、0.18Ω/kmとなっています。そして、fa間は400mで、ab間は800mなので、以下の計算結果を上図に記載しています。

電流I_abについては以下の計算によって求めます。

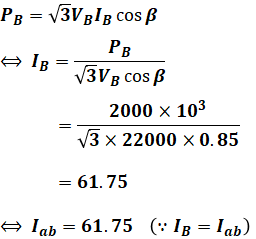
この条件において、a-b間の電圧降下V_abは以下の式で求めることができます。

電圧降下の式は公式として覚えておくことをおすすめします(ベクトル図を描いて式を導出することもできますが、頻出なので覚えたほうがよいと思います。導出方法は気になる方は、三相3線式送電線の電圧降下を参照してください)。

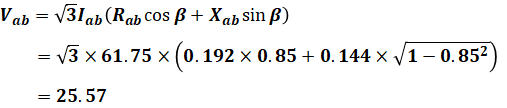
よって、aの位置の電圧は約22026Vとなります。

一方、電流I_faの大きさを知るためには、I_Aの大きさを知る必要があります(I_abは既知なので)。I_Aの大きさは、(a)で使った図より、皮相電力S_A=3800kV・Aなので、

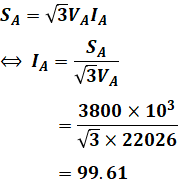
となります。

これでI_abとI_Aがわかったので、これらを合わせればI_faの大きさを求めることが、I_abとI_Aはベクトルの向きがずれているので、そのまま足すことはできません。よって、次のようにしてI_faの大きさを計算します。

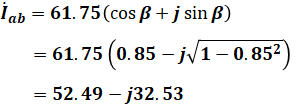
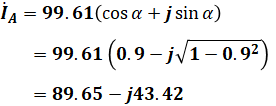
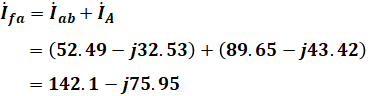
あとはa-b間の電圧降下を求めたときと同じように、f-a間の電圧降下V_faを求めます。

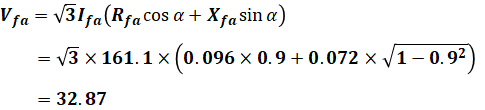
以上から、f-b間の電圧降下V_fbは、

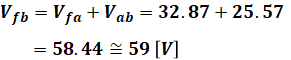
と計算することができます。