問 題
図1の端子a-d間の合成静電容量について、次の(a)及び(b)の問に答えよ。
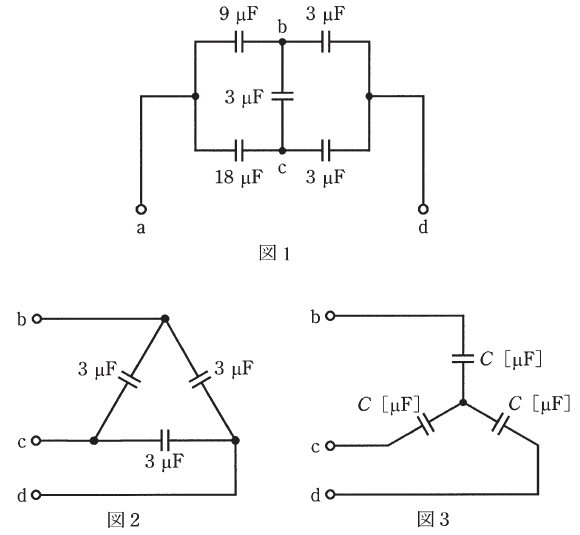
(a) 端子b-c-d間は図2のようにΔ結線で接続されている。これを図3のようにY結線に変換したとき、電気的に等価となるコンデンサCの値[μF]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 1.0
- 2.0
- 4.5
- 6.0
- 9.0
(b) 図3を用いて、図1の端子b-c-d間をY結線回路に変換したとき、図1の端子a-d間の合成静電容量C0の値[μF]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 3.0
- 4.5
- 4.8
- 6.0
- 9.0
解 説
(a)
Δ結線をY結線に変換する際、コンデンサの静電容量は3倍になります。よって、図2のΔ結線を図3のY結線に変換したとき、コンデンサCの値は3[μF]の3倍である9.0[μF]となります。
よって、正解は(5)です。
もしくは、Δ結線をY結線に変換する際にインピーダンス(抵抗、コイルのリアクタンス、コンデンサのリアクタンス)が3分の1となることを覚えているのであれば、
![]()
より、コンデンサのリアクタンスが3分の1になるなら静電容量は3倍になるはずなので、上記と同様、C=9.0[μF]と導くこともできます。
(b)
問題文より図3を図1に反映させるということなので、そのようにすると以下のような等価回路が描けます(以下の図では色々と記入していますが、この段階では黒色にだけ注目してください)。
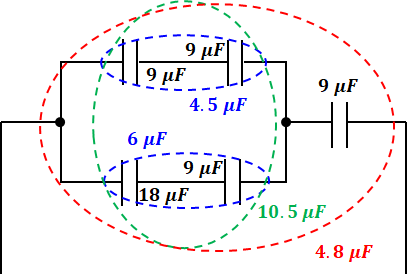
端子a-d間の合成静電容量C0の値は、上図の青色 → 緑色 → 赤色の順に合成していくことで求めることができます。
まず、青色部分は、2つのコンデンサが直列に並んでいるので、次の計算により合成します。
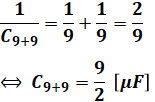
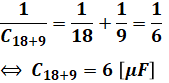
続いて緑色部分について、上記で合成した2つのコンデンサは並列に並ぶので、単純に足し算で合成できます。
![]()
最後に赤色部分ですが、上記で求めたコンデンサと一番右端のコンデンサは直列なので、以下のように計算すれば、求める合成静電容量C0の値が算出できます。
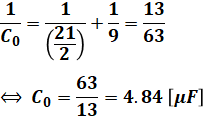
以上より、正解は(3)となります。

コメント