問 題
次の文章は、単相変圧器の電圧変動に関する記述である。
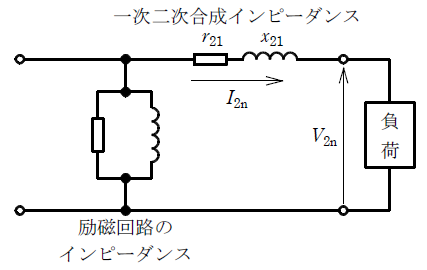
単相変圧器において、一次抵抗及び一次漏れリアクタンスが励磁回路のインピーダンスに比べて十分小さいとして二次側に移した、二次側換算の簡易等価回路は図のようになる。r21=1.0×10-3Ω、x21=3.0×10-3Ω、定格二次電圧V2n=100V、定格二次電流I2n=1kAとする。
負荷の力率が遅れ80%のとき、百分率抵抗降下p、百分率リアクタンス降下q及び電圧変動率εのそれぞれの値[%]の組合せとして、最も近いものを次の(1)~(5)のうちから一つ選べ。なお、本問では簡単のため用いられる近似式を用いて解答すること。
p q ε
- 3.0 1.0 3.0
- 3.0 1.0 2.4
- 1.0 3.0 3.1
- 1.0 2.6 3.0
- 1.0 3.0 2.6
正解 (5)
解 説
変圧器の電圧変動率を求める式は以下の通りです。これは正確な変動率ではなく近似式なのですが、今回の問題文にもある通り、電験三種の試験では近似式を使うことが求められますので、この式を公式として押さえてください。
![]()
- ε:電圧変動率[%]
- p:百分率抵抗降下(パーセント抵抗)[%]
- q:百分率リアクタンス降下(パーセントリアクタンス)[%]
- cosθ:力率
![]()
- I2n:定格運転時の二次電流[A]
- r21:二次側に換算した等価回路の抵抗[Ω]
- x21:二次側に換算した等価回路のリアクタンス[Ω]
- V2n:定格運転時の二次電圧[V]
以上の式に問題文で与えられた数値を代入していけば答えを求めることができます。
まず、pとqを計算すると以下のようになります。
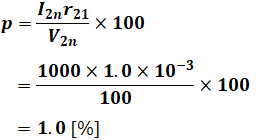
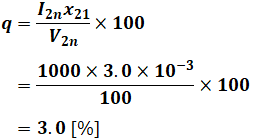
続いてεを計算したいのですが、そのためにはcosθとsinθの値が必要です。cosθは問題文の「負荷の力率が遅れ80%」から、cosθ=0.8とわかるので、以下のようにしてsinθを計算します。
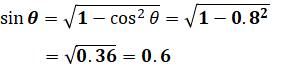
以上から、εは次のように計算できます。
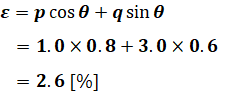

コメント