問 題
図に示すように、中性点をリアクトルLを介して接地している公称電圧66kVの系統があるとき、次の(a)及び(b)の問に答えよ。なお、図中のCは、送電線の対地静電容量に相当する等価キャパシタを示す。また、図に表示されていない電気定数は無視する。
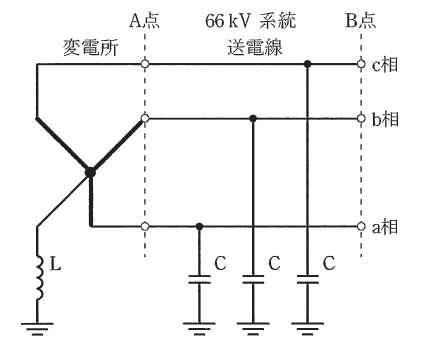
(a) 送電線の線路定数を測定するために、図中のA点で変電所と送電線を切り離し、A点で送電線の3線を一括して、これと大地間に公称電圧の相電圧相当の電圧を加えて充電すると、一括した線に流れる全充電電流は115Aであった。
このとき、この送電線の1相当たりのアドミタンスの大きさ[mS]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 0.58
- 1.0
- 1.7
- 3.0
- 9.1
(b) 図中のB点のa相で1線地絡事故が発生したとき、地絡点を流れる電流を零とするために必要なリアクトルLのインピーダンスの大きさ[Ω]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、送電線の電気定数は、(a)で求めた値を用いるものとする。
- 111
- 196
- 333
- 575
- 1000
解 説
(a)を解く前に、まず確認しておきたいのが、アドミタンスY[S](単位:ジーメンス)とは、インピーダンスZ[Ω]の逆数です。
たとえば、電流I[A]は、電圧E[V]とインピーダンスZ[Ω]から求めることができる一方、アドミタンスY[S]を使うこともできます。
![]()
そのため、アドミタンスで表すことのできる式は全てインピーダンスで表すことができますが、インピーダンスを使うと分数の計算が煩雑になりそうな場合など、アドミタンスを使ったほうが便利なこともあります。
以上を踏まえて、問題の解説を始めます。
(a)
この問題ではA点で3線をつないで、そこに公称電圧66[kV]の電圧を掛けているので、1相分の等価回路は次の図のように描くことができます。
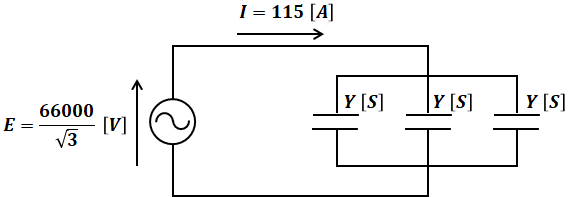
上図を見ると、この問題でインピーダンスではなくアドミタンスの話を持ち出している意味がわかります。つまり、インピーダンスの合成は直列だと足し算ができる一方、並列では逆数の和から計算しなくてはいけません。
しかし、アドミタンスを使えば、並列に並んだコンデンサ(キャパシタ)の合成アドミタンスが単純な和で計算できます。この問題において1相あたりのアドミタンスをY[S]とすると、3つ合わせて3Y[S]となるので、I、E、Yの関係式は以下のように表すことができ、Yについて解くと答えが出ます。
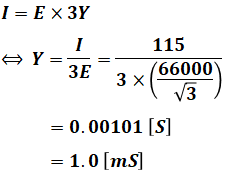
(b)
コイルとコンデンサが並列に並んだ回路では、コイルのリアクタンス(誘導性リアクタンス)とコンデンサのリアクタンス(容量性リアクタンス)の大きさが等しいとき、これらが打ち消し合って電流が流れなくなります(合成したアドミタンスが0になる=逆数であるインピーダンスが∞となるので、電流が流れません)。
このような現象のことを「並列共振」といいます。
少し脱線しますが、直列に並んでいるときにコイルとコンデンサのリアクタンスが等しいときには、合成したインピーダンスが0になるため、この場合は電流ではなく電圧が0になります(大電流が流れます)。こちらの場合は「直列共振」と呼ばれる現象です。
話を戻すと、この問題では地絡電流を0にしたいということなので、並列共振が起これば良いということになります。求めるインピーダンスの大きさは、
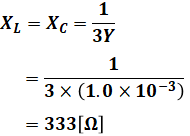
- XL:リアクトル(コイル)のインピーダンス(リアクタンス)[Ω]
- XC:キャパシタ(コンデンサ)のインピーダンス(リアクタンス)[Ω]
となります。

コメント