問 題
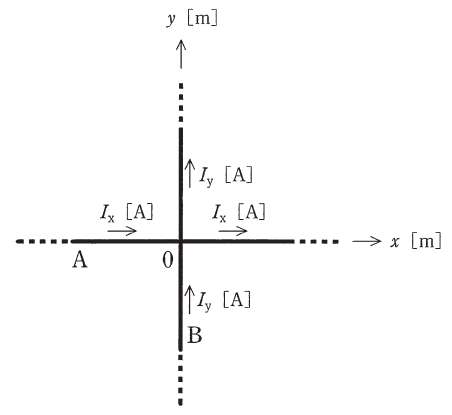
図のように、十分に長い直線状導体A、Bがあり、AとBはそれぞれ直角座標系のx軸とy軸に沿って置かれている。Aには+x方向の電流Ix[A]が、Bには+y方向の電流Iy[A]が、それぞれ流れている。Ix>0、Iy>0とする。このとき、xy平面上でIxとIyのつくる磁界が零となる点(x[m]、y[m])の満たす条件として、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、x≠0、y≠0とする。
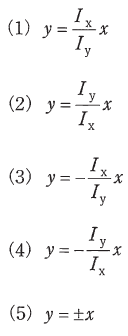
解 説
まずは磁界が0となる点がxy平面上のどのあたりになるかについて考えます(正確な距離感は後回しにします)。
直線状導体を流れる磁界の向きは右ねじの法則に従うため、問題文の図にその向きを記入すると以下のようになります(○の中に●があるのは奥から手前、○の中に×があるのは手前から奥、を表す記号です)。
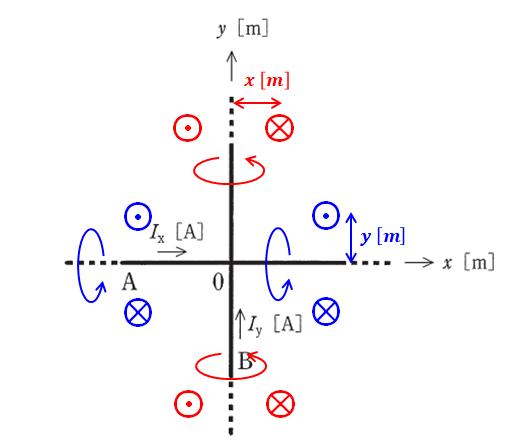
磁界が0になる点は、上図のうち、Ixがつくる磁界(青色)とIyがつくる磁界(赤色)が打ち消し合うところなので、第1象限(右上)と第3象限(左下)となります。
この時点で、正解の選択肢は(1)か(2)に絞られます。
なぜなら、(1)と(2)は原点を通って傾きが正の直線になるので、第1象限(右上)と第3象限(左下)を通るからです。一方、(3)と(4)は傾きが負の直線になるので、これでは第2象限(左上)と第4象限(右下)を通ってしまいます。また、(5)は原点を中心とした×マークのように、2本の直線を表します。つまり、これは全ての象限を通ります。
続いて、今度は具体的に、磁界の強さと距離について考えます。
十分に長い直線状導体の磁界の強さH[A/m]は、電流I[A]と距離r[m]から次の式で示されます。
![]()
よって、IxとIyのつくる磁界が0となるためには、第1象限(第3でもいいです)の青い磁界の強さと赤い磁界の強さが一致すればよいです。青い磁界と赤い磁界は向きが反対なので、強さが一致すれば、それらを重ね合わせた磁界は0となります。これを式にして、yについて解いたのが以下の式です。
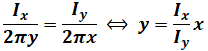
以上から、答えが(1)とわかります。

コメント