問 題
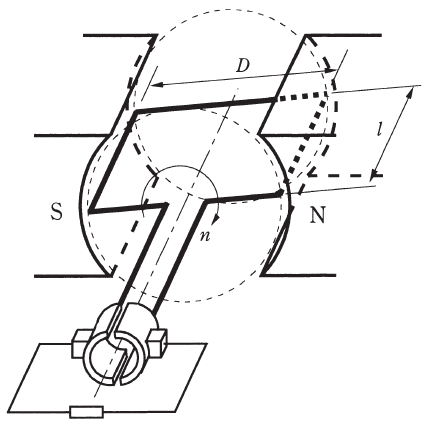
図は、磁極数が2の直流発電機を模式的に表したものである。電機子巻線については、1巻き分のコイルを示している。電機子の直径Dは0.5[m]、電機子導体の有効長lは0.3[m]、ギャップの磁束密度Bは、図の状態のように電機子導体が磁極の中心付近にあるとき一定で0.4[T]、回転速度nは1200[min-1]である。
図の状態におけるこの1巻きのコイルに誘導される起電力e[V]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 2.40
- 3.77
- 7.54
- 15.1
- 452
正解 (3)
解 説
直流発電機は、フレミングの右手の法則に従って動くため、これを使って計算します。フレミングの右手の法則とは、長さl[m]の導体を磁束密度B[T]の磁束の方向と直角に置き、速度v[m/s]で導体と磁束の両方に直角な方向に移動させると、導体にe=Blv[V]の誘導起電力が発生するという法則です。
Bとlは問題文で与えられていますが、vが不明なので、vを以下の式によって計算します。
![]()
上式のπDは、電機子が回転する際の1周分の軌跡の円周で、n/60は1秒あたりの回転数です。
よって、あとは最初に示した式によってeを計算します。ちなみに、係数の2について、誘電起電力が発生する場所が問題文の右側(N極側)のlと記入されている部分だけでなく、反対側(S極側)の同様の部分にも同じだけの誘電起電力が発生するため、合わせて2としています。
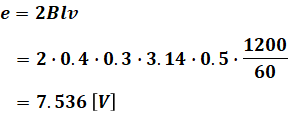

コメント