問 題
復水器の冷却に海水を使用する汽力発電所が定格出力で運転している。次の(a)及び(b)の問に答えよ。
(a) この発電所の定格出力運転時には発電端熱効率が38[%]、燃料消費量が40[t/h]である。1時間当たりの発生電力量[MW・h]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、燃料発電量は44000[kJ/kg]とする。
- 186
- 489
- 778
- 1286
- 2046
(b) 定格出力で運転を行った時、復水器冷却水の温度上昇を7[K]とするために必要な復水器冷却水の流量[m3/s]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、タービン熱消費率を8000[kJ/(kW・h)]、海水の比熱と密度をそれぞれ4.0[kJ/(kg・K)]、1.0×103[kg/m3]、発電機効率を98[%]とし、提示していない条件は無視する。
- 6.8
- 8.0
- 14.8
- 17.9
- 21.0
解 説
(a)
燃料を1時間に40[t](=40×103[kg])使っているので、その燃料発熱量は、1時間あたり
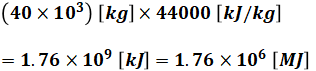
となります。
また、発電端効率が38[%]なので、1時間あたりの発生電力量は、
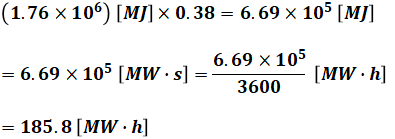
となります(「秒」を「時間」に換算するために3600で割っています)。
(b)
この問題は、タービンから復水器に送られる毎時熱量q'[kJ/h]と、復水器冷却水が冷却により受け取る毎時熱量H[kJ/h]が等しくなる点に注目して、双方の式をイコールで結んで計算していけば解くことができます。
まずは、タービンから復水器に送られる毎時熱量q'[kJ/h]について考えます。タービンに入ってくる(入力)毎時熱量をqin[kJ/h]とし、出力をqout[kJ/h]とすると、
![]()
が成り立ちます。
ここで、qout[kJ/h]は、発生電力量P[kW]と発電効率η[%]を使って次のように求めることができます。右辺の右側の分数(電力÷効率)がタービン出力[kW]に相当します。右辺の左側の係数は、[kW]=[kJ/s]を[kJ/h]に直すために掛けています。
ちなみに、Pは設問(a)の答えの数値で、ηは問題文に98[%]とありますが、計算はあとでまとめてやります(好みの問題なので、できるところから数字を入れて計算していっても構いません)。
![]()
また、qin[kJ/h]は、タービン熱消費率j[kJ/(kW・h)]とタービン出力[kW]の積なので、次のようになります。
![]()
よって、q'[kJ/h]は次の式で表すことができます。
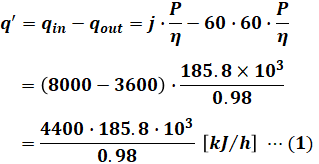
一方、復水器冷却水が冷却により受け取る毎時熱量H[kJ/h]は、次の式の通りです。
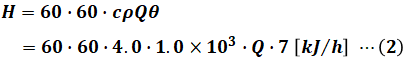
- c:海水の比熱 4.0[kJ/(kg・K)]
- ρ:海水の密度 1.0×103[kg/m3]
- Q:復水器冷却水の流量[m3/s]
- θ:復水器冷却水の温度上昇 7[K]
あとは(1)式と(2)式をイコールでつなぎ、計算を進めていけば求めるQ[m3/s]が算出できます。
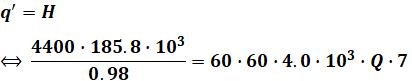
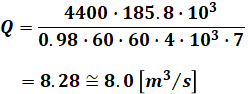

コメント