問 題
三相3線式1回線無負荷送電線の送電端に線間電圧66.0[kV]を加えると、受電端の線間電圧は72.0[kV]、1線当たりの送電端電流は30.0[A]であった。この送電線が、線路アドミタンスB[mS]と線路リアクタンスX[Ω]を用いて、図に示す等価回路で表現できるとき、次の(a)及び(b)の問に答えよ。
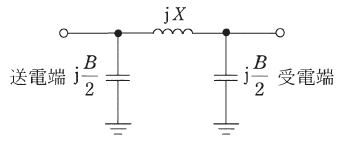
(a) 線路アドミタンスB[mS]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 0.217
- 0.377
- 0.435
- 0.545
- 0.753
(b) 線路リアクタンスX[Ω]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 222
- 306
- 384
- 443
- 770
解 説
(a)を解く前に、まず確認しておきたいのが、アドミタンスY[S](単位:ジーメンス)とは、インピーダンスZ[Ω]の逆数です。たとえば、電流I[A]は、電圧E[V]とインピーダンスZ[Ω]から求めることができる一方、アドミタンスY[S]を使うこともできます。
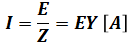
そのため、アドミタンスで表すことのできる式は全てインピーダンスで表すことができますが、インピーダンスを使うと分数の計算が煩雑になりそうな場合など、アドミタンスを使ったほうが便利なこともあります。
以上を踏まえて、問題の解説を始めます。
(a)
問題文で与えられている数値を図に記入していくと、下図のような感じになります。
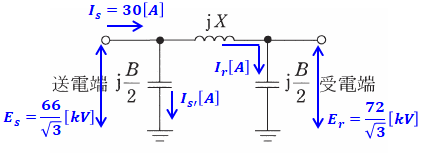
ここで、電流Is[A]は以下の式で表すことができます。
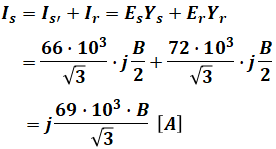
Is=30.0[A]なので、求めるB[mS]は次のように計算することができます。
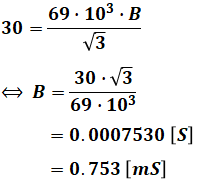
(b)
まず最初に(a)の計算結果を使って線路を流れる電流Ir[A]を求めます。
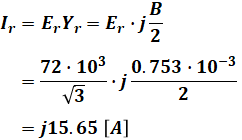
また、線路の電圧降下は次の式で表すことができます。これは公式として覚えておきたい知識ですが、導出過程が気になる方は三相3線式送電線の電圧降下のページを参照してください。
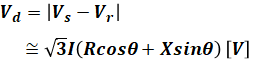
- Vd:電圧降下[V]
- Vs:送電端電圧[V]
- Vr:受電端電圧[V]
- I:線電流[A]
- R:抵抗(電線1条あたり)[Ω]
- X:リアクタンス(電線1条あたり)[Ω]
- cosθ:負荷の力率
ただし、今回は抵抗Rがないので、sinθ=1となります。
よって、以下のように計算をすれば、線路リアクタンスX[Ω]を求めることができます。
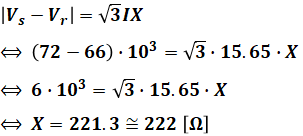

コメント