問 題
図のように、相電圧200[V]の対称三相交流電源に、複素インピーダンス![]() の負荷がY結線された平衡三相負荷を接続した同路がある。次の(a)及び(b)の問に答えよ。
の負荷がY結線された平衡三相負荷を接続した同路がある。次の(a)及び(b)の問に答えよ。
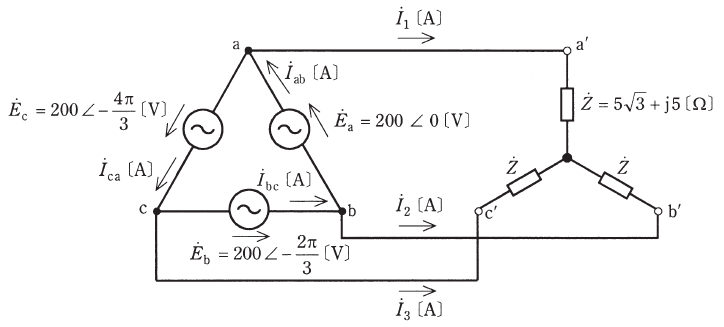
(a) 電流I1[A]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
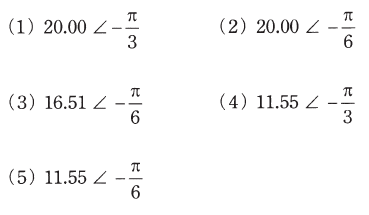
(b) 電流Iab[A]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
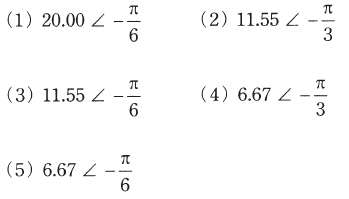
解 説
(a)
Δ-Y結線のままでは計算しづらいので、Δ結線をY結線に変換して、Y-Y結線にして考えると良いです。以下、Y-Y結線での解説となりますが、統一さえすれば、Δ-Δ結線で考えても問題ありません(個人的には、Y-Y結線のほうが中性線を使った1相あたりの等価回路が描けるので、理解しやすいと思います)。
Y-Y結線にして中性線で結んだ1相分の等価回路は次のように描くことができます。
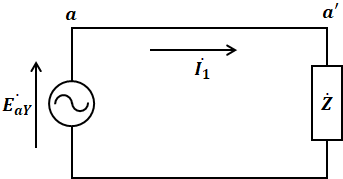
ここで、Δ結線をY結線に変換する際、1相あたりの電圧の大きさは√3分の1になり、位相はπ/6[rad](=30°)遅れるので、変換後の電圧は次のようになります。
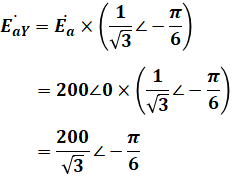
また、問題分には複素インピーダンスが複素数の形で表示されているので、これを電圧と同じ形に直します。
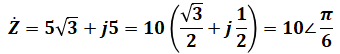
ちなみに、上式でくくる数を10にしているのは、( )内の大きさ(絶対値)を1にしたかったからです。
というのも、この問題では問題の図に記載されている式も、(a)の選択肢でも、全て「大きさ・位相」の形で表記されています。たとえばこの式を5でくくってしまうと、( )内の数値の大きさが1にならず、その次の段階で「∠」(角記号)を用いた式に書き換えられません。よって、ここでは10でくくっています(5√3の2乗+5の2乗=100より、√100=10という流れです)。
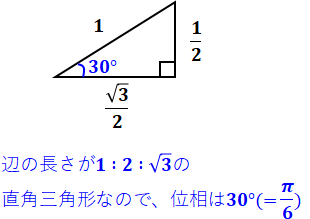
また、(√3/2+j1/2)の部分は位相で表すといくつになるのかという話ですが、以下のような直角三角形を描けば、3辺が1:2:√3の直角三角形になるので、位相は30°(=π/6)であることがわかります。
以上より、電流I1は次のように計算することができます(ちなみに、ベクトルの割り算では、角度の部分は引き算をします)。
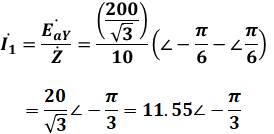
よって、正解は(4)となります。
(b)
Iabが問われていますが、すでに(a)でI1を求めているので、これを利用します。以下の図が描ければすぐに答えはわかりますが、この図の書き方を①~⑥の順番で説明していきます。
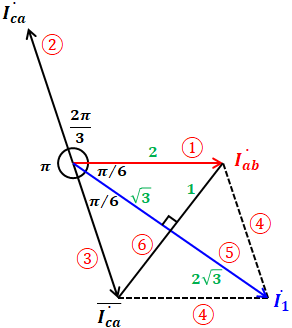
まず、①は求めるべきIabの矢印を描きます。この段階では何もわからないので、長さも向きも適当で構いません。
最初に説明したように、IabとI1との関係を見出すことが目的ですが、問題文の図より、I1=Iab-Icaであることがわかるので、続いて②としてIcaを記入します。
IabとIcaは長さが一緒で、角度は+方向に2π/3[rad](=+120°)です(問題文の図では-4π/3[rad]となっていますので、正確には反時計周りに240°ですが、+120°と同じことです)。
I1=Iab-Icaより、I1を描くためにはIcaの符号はマイナスにしたいので、③のようにIcaを反対にします。
以上より、Iab(①)と-Ica(③)の合力がI1になるので、①や③を平行移動した④の線を書いて平行四辺形を作り、その対角線である⑤がI1を表すベクトルとなります。ちなみに、もう一方の対角線⑥を書くと、対角線同士が直交するので直角三角形が見えてきます。
ここで、①と③の角度はπ/3(∵2π-2π/3-π=π/3)なので、Iab(赤矢印)とI1(青矢印)とがなす角は、その半分のπ/6(=30°)になります。よって、Iab(赤矢印)を含む直角三角形の辺の長さは緑色で示したように1:2:√3の関係となり、また、そのときI1の大きさは2√3であることがわかります。
以上から、IabはI1に比べて、大きさが2/(2√3)で、角度がπ/6(=30°)だけ進んでいることがわかるので、
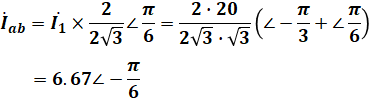
と計算することができます。
よって、正解は(5)です。
【別解】
上記の解説で示したようなベクトル図を書くのが苦手な場合、以下のように考えてもこの問題を解くことができます。
まず、(a)により線電流I1は次の通りです。
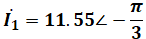
求めたいのは電源側の相電流Iabですが、三相交流回路のΔ結線の場合、線電流は相電流の√3倍の大きさで、位相は相電流よりもπ/6[rad](30°)の遅れとなります。これは重要事項として覚えておきたい知識です。詳しくは相電圧と線間電圧、相電流と線電流のページを参照してください。
よって、この問題の場合、相電流Iabは線電流I1に対して大きさが√3分の1で、位相がπ/6[rad](30°)の進みとなります。
以上より、Iabは、
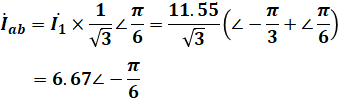
というような計算で求めることができるため、正解は(5)となります。

コメント