問 題
次の文章は、図に示す「磁界中における電子の運動」に関する記述である。
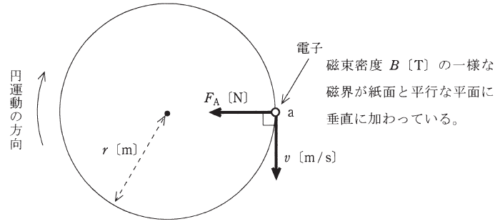
真空中において、磁束密度B[T]の一様な磁界が紙面と平行な平面の( ア )へ垂直に加わっている。ここで、平面上の点aに電荷-e[C]、質量m0[kg]の電子をおき、図に示す向きに速さv[m/s]の初速度を与えると、電子は初速度の向き及び磁界の向きのいずれに対しても垂直で、図に示す向きの電磁力FA[N]を受ける。
この力のために電子は加速度を受けるが速度の大きさは変わらないので、その方向のみが変化する。したがって、電子はこの平面上で時計回りに速さv[m/s]の円運動をする。
この円の半径をr[m]とすると、電子の運動は、磁界が電子に作用する電磁力の大きさFA=Bev[N]と遠心力![]() とが釣り合った円運動であるので、その半径はr=( イ )[m]と計算される。したがって、この円運動の周期はT=( ウ )[s]、角周波数はω=( エ )[rad/s]となる。
とが釣り合った円運動であるので、その半径はr=( イ )[m]と計算される。したがって、この円運動の周期はT=( ウ )[s]、角周波数はω=( エ )[rad/s]となる。
ただし、電子の速さv[m/s]は、光速より十分小さいものとする。また、重力の影響は無視できるものとする。
上記の記述中の空白箇所(ア)、(イ)、(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。

解 説
磁界中を電荷が動くとき、その電荷は磁界からローレンツ力という電磁力を受けます。このローレンツ力の方向を見定めるのに便利なのが、フレミングの左手の法則です。
ローレンツ力の向きに関するパラメータには、「ローレンツ力(電磁力)」、「電流」、「磁界」の3つの向きがあり、左手の親指と人差し指と中指をそれぞれ垂直方向となるようにしたとき、指と各パラメータの向きは次のように対応します。
- 親指:ローレンツ力の向き
- 人差し指:磁界の向き
- 中指:電流の向き
ただし、この問題では「電流」という表現ではなく「電子」と書いてあることに注意してください。電子が流れているものが電流ですが、電子の流れと電流の向きとは反対向きになります。
ここで、図のFAに親指を合わせ、vの反対方向に中指を合わせると、人差し指は平面のおもてから裏への向きを指します。よって、( ア )には「おもてから裏」が入ります。
( イ )は問題文にFAとFBの式が与えられていて、それが釣り合っているという話なので、両式の右辺同士をイコールで結んでrについて解けば答えが出ます。
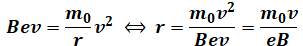
T=( ウ )は、選択肢にある式を見ると、r=( イ )に似た式であることがわかるので、これはTを、rを使った式として表す必要があり、以下の3つの式を組み合わせます。

- T:周期[s]
- f:周波数[Hz]
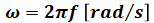
- ω:角周波数[rad/s]
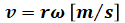
- v:速度[m/s]
- r:半径[m]
以上の3式と( イ )から、Tは次のように計算できます。
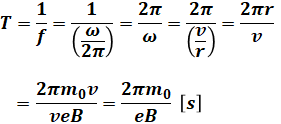
( エ )についても先ほどの式と( ウ )から計算することができます。


コメント