問 題
真空中に、2本の無限長直線状導体が20[cm]の間隔で平行に置かれている。一方の導体に10[A]の直流電流を流しているとき、その導体には1[m]当たり1×10-6[N]の力が働いた。他方の導体に流れている直流電流I[A]の大きさとして、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、真空の透磁率はμ0=4π×10-7[H/m]である。
- 0.1
- 1
- 2
- 5
- 10
正解 (1)
解 説
平行な2本の無限長直線状導体の間に働く1mあたりの力F[N/m]の式は以下のように表されます。
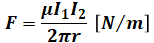
- F:導体間に働く1mあたりの力[N/m]
(電流の向きが一緒なら斥力、反対なら引力) - μ:透磁率4π×10-7[H/m]
- I:電流[A]
- r:導体間の距離[m]
この式を公式として覚えている場合は、問題文で与えられている数値を代入すれば答えを出せます。
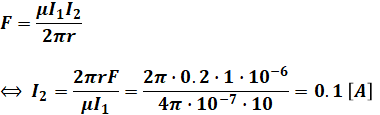
この式は比較的頻出なので、できれば公式として暗記することをお勧めしますが、もし暗記に頼らない場合は、以下のような計算をすることで導出することもできます(上式を公式として覚えられる方は、以下の解説は気にしなくて構いません)。
まず、直線導体を流れる電流がつくる磁界Hは、以下の式で表されます。

- H:磁界[A/m]
- I:電流[A]
- r:導体と磁界の距離[r]
また、磁束密度B[T]は、磁界H[A/m]と透磁率μ[H/m]との積で求められます。
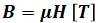
ここで、上記の磁界と同じ距離にもう一つの導体があるとして、その導体を流れる電流が磁界から受ける力F[N]は、フレミングの左手の法則より、次のようになります(以下、2つの電流を区別するため、最初の導体を流れる電流をI1、他方をI2とします)。
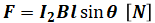
ただし、上式のうちl(エル)は力を受ける導体の長さですが、今回は「1mあたり」という話なのでこれは1となり、また、sinθはBとI2との角度なので今回は垂直で、sin90°=1となるため、これらは計算から除外できます。
よって、この式と先ほどの式を合わせると、以下のようになって、最初に示した公式が導出できます。
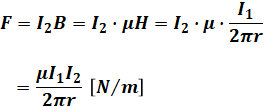

コメント