トルク-回転速度曲線
以下の図は、誘導電動機のトルク-回転速度曲線といわれるものです。
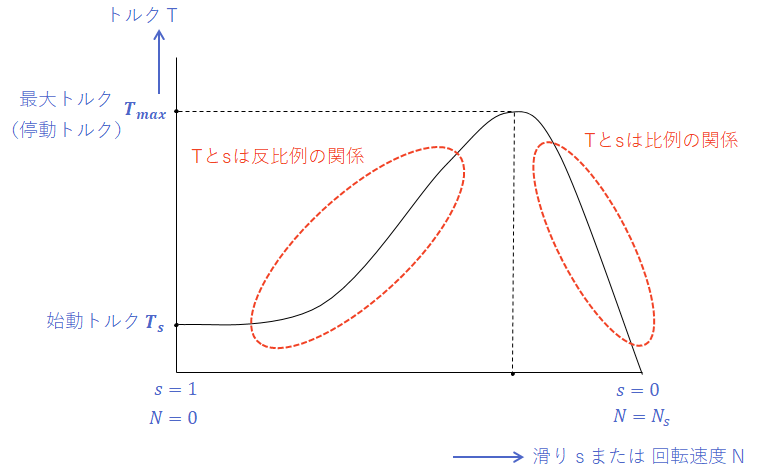
これは、電源電圧と電源周波数が一定の条件の下で、発生するトルクと回転速度との関係を表したグラフになります。
まず、図中の横軸についてですが、これは回転速度Nで表すこともできますが、滑りsで表すこともできます。回転速度Nで表す場合は、一番小さい値(原点)が0となり、一番大きな値が同期速度と同じNsとなります。また、滑りsで表す場合は、原点が最も大きい1となり、右端が最も小さい0をとることになります。
図を見てもわかる通り、滑りsがある値をとったときにトルクTが最大になるという点があります。このときのトルクのことを、最大トルクまたは停動トルクといいます。図中ではTmaxと表記しているところです。
この最大トルク(停動トルク)の前後で、グラフの形が変わっている点にも注意が必要です。ここより手前の部分のグラフは、回転速度が小さいことから、誘導機の始動後まもない状態であることがわかります。この部分では、トルクTと滑りsとの間には、反比例の関係が成り立ちます。
また、最大トルク(停動トルク)よりも右側の部分は、ほぼ右肩下がりの直線的になっています。ここから、回転速度が大きいときには、トルクTと滑りsとの間には、比例の関係が成り立つことが読み取れます。
トルクの式
誘導電動機のトルクTは、同期速度Nsと二次入力P2を使って計算することができます。以下の式は計算問題の際に必要となることもあるので、ぜひ公式として押さえておいてください。
![]()
- T:誘導電動機のトルク[N・m]
- P2:二次入力[W]
- Ns:同期速度[min-1]
もしこの式をそのまま暗記することが難しければ、以下の式変換を参考にしてください(上式を覚えられるなら、次の式は特に気にする必要はありません)。
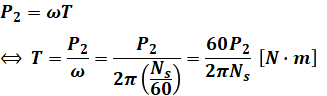
比例推移
巻線形誘導電動機のトルクは、二次回路の巻線抵抗r2と滑りsの比に関係するので、二次回路の巻線抵抗r2がk倍になると、k倍になる前のトルクと同じ大きさのトルクを得るための滑りsも、前の滑りのk倍の点となります。
このように、一定のトルクを生じるための二次巻線抵抗r2と滑りsとの間には比例関係があり、このような特性を比例推移といいます。この特性は、巻線形誘導電動機の始動トルクの改善や速度制御に広く利用されています。
![]()
- r2:二次巻線抵抗[Ω]
- s:滑り
- k:任意の倍数
- const.:一定、という意味(コンスタントの略)
ちなみに、かご形誘導電動機では二次側の抵抗を変えることが難しいので、こちらは比例推移が使えません。

コメント