電験三種 R5年度上期 理論 問17 問題と解説

　問 題　　　　　

図のように、極板間の厚さd[m]、表面積S[m²]の平行板コンデンサAとBがある。

コンデンサAの内部は、比誘電率と厚さが異なる3種類の誘電体で構成され、極板と各誘電体の水平方向の断面積は同一である。

コンデンサBの内部は、比誘電率と水平方向の断面積が異なる3種類の誘電体で構成されている。

コンデンサAの各誘電体内部の電界の強さをそれぞれE_A1、E_A2、E_A3、コンデンサBの各誘電体内部の電界の強さをそれぞれE_B1、E_B2、E_B3とし、端効果、初期電荷及び漏れ電流は無視できるものとする。

また、真空の誘電率をε₀[F/m]とする。両コンデンサの上側の極板に電圧V[V]の直流電源を接続し、下側の極板を接地した。

次の(a)及び(b)の問に答えよ。

(a)　コンデンサAにおける各誘電体内部の電界の強さの大小関係とその中の最大値の組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

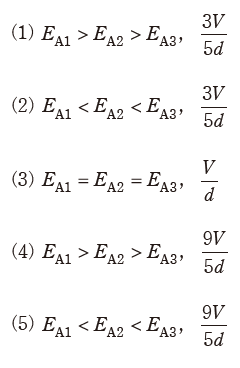
(b)　コンデンサA全体の蓄積エネルギーは、コンデンサB全体の蓄積エネルギーの何倍か、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 0.72
2. 0.83
3. 1.00
4. 1.20
5. 1.38

 

 

 

 

 

　解 説　　　　

(a)

コンデンサAは、3種類の誘電体が電圧の向きから見て縦に並んでいるため、下図のように3つのコンデンサが直列に並んでいるのと同等です。また、直列に並んだコンデンサに蓄えられる電荷Q[C]は、全て等しくなります。

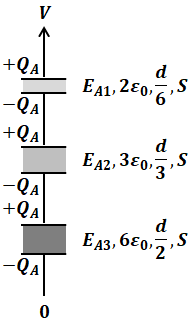
ここで、問われているのは電界の強さの大小関係ですが、電界E[V/m]は次の式で求めることができます。

• E：電界の強さ [V/m]
• V：電圧 [V]
• d：板間距離 [m]

また、電圧V[V]は電荷Q[C]と静電容量C[F]を使って以下の等式で表されます。

• Q：電荷[C]
• C：静電容量[F]

さらに、静電容量C[F]は問題文で与えられている各パラメータを使って下式の通り表すことができます。

• ε：誘電率[F/m]
• S：板の面積[m²]
• d：板間距離[m]

(2)式と(3)式を(1)式に代入すると、次のようになります。

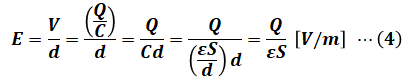
(4)式に上図に書き込んだ各数値を代入することで、電界E_A1、E_A2、E_A3を比較することができます。

よって、それらの比は次のように計算できます。

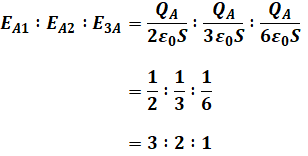
この時点で、選択肢は(1)か(4)に絞られます。

続いて、この中で最も強い電界E_A1の値について考えていきます。

E_A1の式はすでに(5)式で求めていますが、この中の電荷Q_Aは問題文に登場しないパラメータなので、これを問題文で与えられているパラメータで表すのが目標となります。

電荷Q_Aを含む式として、まず(2)式を今回の問題文に合うように書き換えると、次のようになります。

• Q_A：コンデンサAに蓄えられる電荷 [C]
• C_A：コンデンサA全体の静電容量 [C]
• V：コンデンサAの端子電圧 [V]

また、複数のコンデンサが直列に並んでいるとき、合成静電容量の逆数は、各々の静電容量の逆数の和と一致します。よって、3つの誘電体のそれぞれの静電容量をC_A1、C_A2、C_A3とすると、次の等式が成り立ちます。

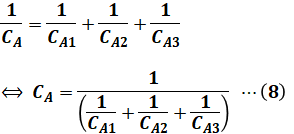
次に、(8)式を(2)’式に代入します。

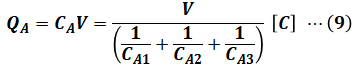
ここで、静電容量の公式である(3)式を使うと、(9)式は次のように計算できます。やや複雑な計算ですが、通分などを慎重に行ってください。

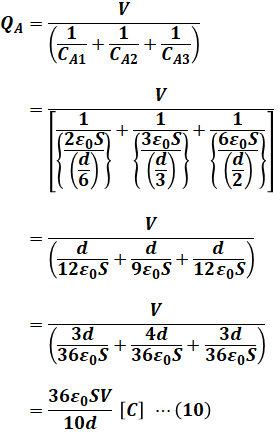
よって、(10)式を(5)式に代入することで、求めたいE_A1を計算することができます。

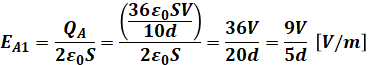
以上から、正解は(4)です。

(b)

コンデンサに蓄えられるエネルギーは、次の式で表すことができます。

• W：エネルギー[J]
• C：静電容量[F]
• V：電圧[V]
• Q：電荷[C]

よって、本問の解法としては、コンデンサA、Bそれぞれのエネルギーを上式を使って求め、それらの比を計算するというアプローチを取ります。

コンデンサAについては、(a)でたくさん計算をしたので、これを利用するべきです。つまり、(11)式の3項に(a)での(10)式を代入すると、コンデンサAのエネルギーW_Aは次のように計算できます。

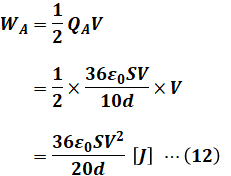
続いてコンデンサBについて考えます。

コンデンサBは、3種類の誘電体が電圧の向きから見て横に並んでいるため、下図のように3つのコンデンサが並列に並んでいるのと同等です。

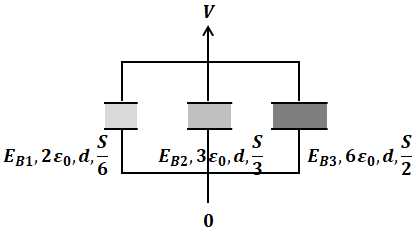
複数のコンデンサが並列に並んでいるとき、その合成静電容量は、各々の静電容量の和と一致します。よって、コンデンサB全体の静電容量をC_B、3つの誘電体のそれぞれの静電容量をC_B1、C_B2、C_B3とすると、次の等式が成り立ちます。

ここで、静電容量の公式である(3)式に上図で示した値を代入し、さらに(13)式に代入すると、以下のようになります。

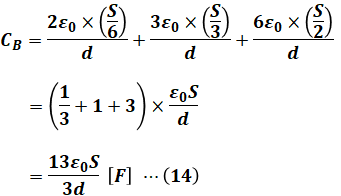
よって、(11)式の2項に(14)式を代入すると、コンデンサBのエネルギーW_Bは次のように計算できます。

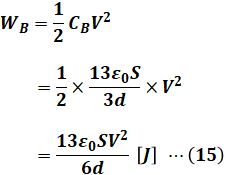
(12)式と(15)式から、コンデンサAとコンデンサBのエネルギー比(＝W_A/W_B)は以下の通りとなります。

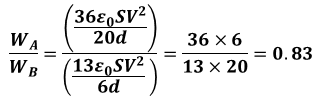
よって、正解は(2)です。