ループ回路(環状配電線路)と分岐回路の電圧降下が計算問題としてよく取り上げられます。
この項では、実際に電験三種の問題として出題されたループ回路を例に、これらの計算方法を解説します。分岐回路の電圧降下については次項で取り上げます。
ループ回路の電圧降下
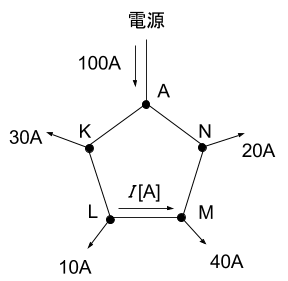
まずは以下の図を見てください。
条件:
- 配電線路は単相2線式1回線
- 点Aにおける線間電圧VA=105[V]
- 回路1線当たりの抵抗は、AK間が0.05[Ω]、KL間が0.04[Ω]、LM間が0.07[Ω]、MN間が0.05[Ω]、NA間が0.04[Ω]
- 負荷の力率は全て100[%]で、線路のリアクタンスは無視できる
上記の条件のとき、点Aにおける線間電圧VAが105[V]だったとしても、配電される過程で少しロスしてしまい、たとえば点Mにおける線間電圧VMは105[V]よりも少し小さい値となります。
これがループ回路の電圧降下で、では実際にVMを計算してみてください、というような計算問題が出題されます。
VMを求めるためには、まず、図中のI[A]を求める必要があります。
点L→点Mを流れる電流がI[A]であれば、図より、点K→点Lを流れる電流は、I+10[A]となります。同様に考えると、点A→点Kを流れる電流は、I+10+30=I+40[A]となります。また、点N→点Aを流れる電流は、I+40-100=I-60[A]となります。さらに、点M→点Nを流れる電流は、I-60+20=I-40[A]となります。
これでそれぞれの区間を流れる電流がわかり、各区間の抵抗はすでに条件として与えられているので、あとは点Aと起点として反時計回りに電流が流れるとすると、キルヒホッフの法則により以下の式が成り立ちます。
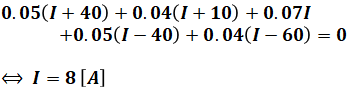
すると、点K→点L、点A→点K、点N→点A、点M→点Nを流れる電流は、上記の「I」に「8」を代入すれば計算でき、それぞれ、18[A]、48[A]、-52[A](時計回り方向に52[A])、-32[A](時計回り方向に32[A])となります。これらを図にまとめると、以下のようになります。

ここまでわかれば、点Aにおける線間電圧VAが105[V]のとき、点A→点N→点Mの過程でロスする電圧を計算すれば良いので、点Mにおける線間電圧VMは
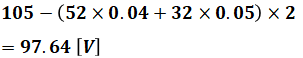
となります。ちなみに、式の最後にある「×2」は、条件のところに記載している通り、配電線路が2線式だからです。
また、上記の計算は点A→点N→点Mの過程のロスを計算しましたが、点A→点K→点L→点Mの軌跡をたどっても、計算量は増えますが、もちろん同じ計算結果が得られます。
ループ回路の電圧降下については上記のように電流と抵抗から電圧を計算することで求められます。類似の問題に対応できるよう、ぜひ計算の流れを覚えておいてください。

コメント