前項ではsinθやcosθの値について、θ=0°、30°、45°、60°、90°のときの値を紹介しました。これさえ押さえておけば大体の計算問題は解けますが、中にはθが90°を超えたり、あるいはマイナスだったりすることもあります。
この項では、θ=0°、30°、45°、60°、90°のときのsinθとcosθの値がわかっていることを前提として、その範囲外のθのときの計算方法について解説します。
まず、三角比(sinとcos)とθとの関係は、以下の図でまとめることができます。
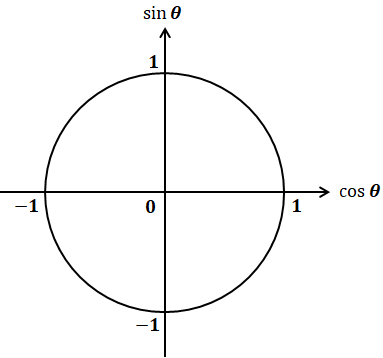
上図のように、座標上に原点を中心とする円を描いたとき、横軸がcosθ、縦軸がsinθとなります。ということは、0°~90°、90°~180°、180°~270°、270°~360°の4つのブロック(象限)において、sinθ(縦軸)とcosθ(横軸)の符号は次のようになることを示しています。
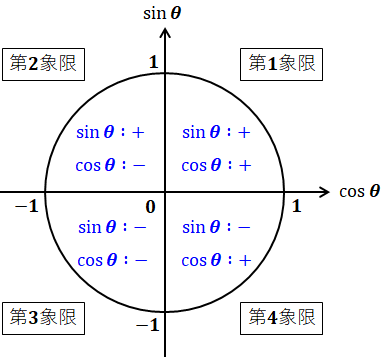
以上のことを押さえておけば、あとはθが120°であっても225°であっても-30°であっても、符号にさえ気をつければ、前項で扱った、θ=0°、30°、45°、60°、90°のどれかと同じ形に当てはめることができます。
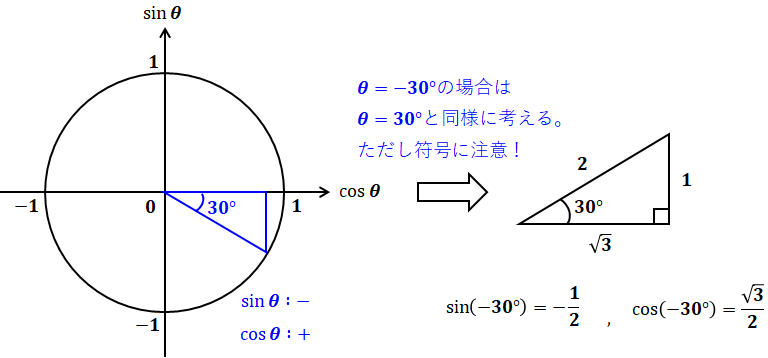
たとえば、上記で示したθ=120°、225°、-30°のsinθとcosθはそれぞれ次のようになります。
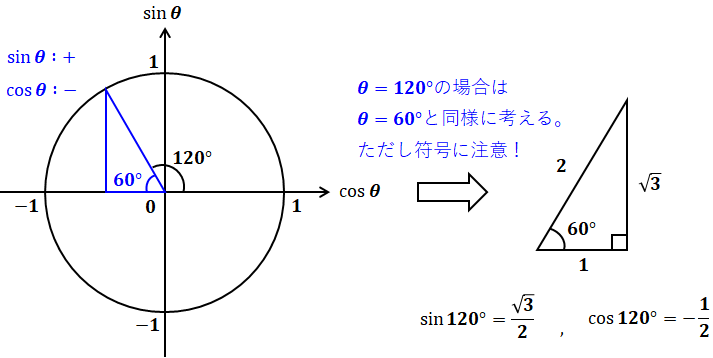
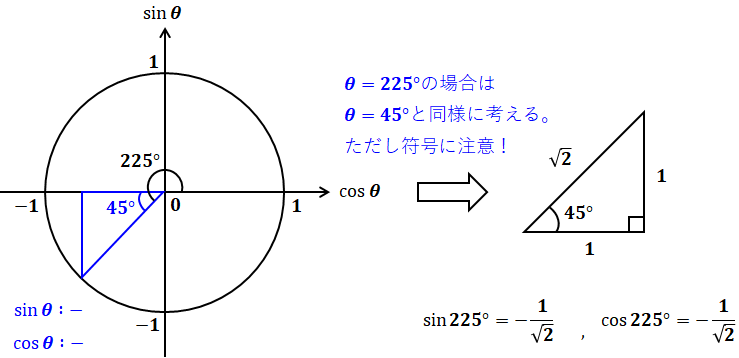

コメント