この項では、sinθ、cosθ、tanθのいずれかの値から、ほかの値を導くための重要公式を紹介します。
もちろん、θが何度なのかわかっていれば、三角比の計算や単位円の図からsinθやcosθ、tanθを求めることができますが、今回は、θの値が具体的にわかっておらず、sinθの値だけ与えられているところからcosθやtanθを求めたいと考えてください。
ぜひ覚えておきたいの最重要公式は、以下の2つです。
![]()
![]()
これさえ押さえておけば、sinθの値だけから、cosθやtanθの値を出すのは簡単です。つまり、1つ目の式を使えばcosθが計算でき、そのあと2つ目の式を使えばtanθの値も導出できます。
cosθの値だけが既知の場合も同様に、1つ目の式でsinθを、続いて2つ目の式を使ってtanθを求められます。
最初に与えられているのがtanθのときは、ちょっと面倒ですが、ここからsinθとcosθを求めることも可能です(計算が煩雑になるからか、出題頻度は低いです)。この場合、まず1番目の式を次のようにsinθについて解き、
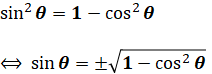
これを2つ目の式に代入すれば、
![]()
上式のようになって、tanθの値を代入すればcosθの値が算出されます。また、1つ目の式に戻れば、cosθからsinθの値もわかります。
このように、最初に紹介した2式を駆使することで、sinθ、cosθ、tanθのどれか1つから、ほかの2つを計算することができるので、これは最重要公式としてしっかり押さえておいてください。
以下に、なぜこの公式が成り立つのかを簡単に説明しますが、この過程については理解してもしなくても構いません。公式を暗記する際のちょっとした参考として、軽い気持ちでお読みください。
まず、1つ目の公式
![]()
についてですが、これは0°未満、90°超の三角比の計算のページで紹介した単位円(原点を中心とした半径1の円)を用いるとわかりやすいです。
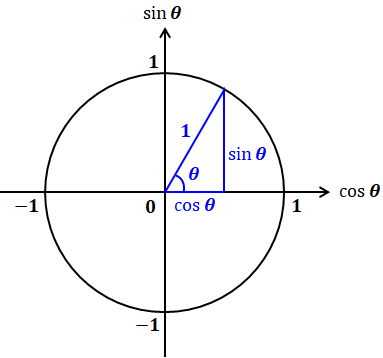
単位円においては、円周上の点(どこでもいいです)の横軸の座標がcosθ、縦軸の座標がsinθとなります。つまり、上図の直角三角形は底辺がcosθ、高さがsinθ、斜辺が1(円の半径)なので、三平方の定理より、
![]()
が成り立ちます。この式が1つ目の公式です。
続いて、2つ目の公式
![]()
についてですが、そもそもtanθの定義は、角度の表し方と三角比の基礎のページで紹介したように、直角三角形における「(高さ)/(底辺)」です。よって、これも上図に示した単位円に描いた直角三角形を見ればわかる通り、底辺がcosθで、高さがsinθなので、
![]()
が成り立ちます。これが2つ目の公式の理屈です。
繰り返しになりますが、導出過程は重要ではありませんが、この計算式自体はとても重要です。2つの式は、公式としてきちんと覚えておくことをお勧めします。

コメント