抵抗R[Ω]とリアクタンスX[Ω]の合成インピーダンスZは次のように複素数で表すことができます(このあたりの基本的な考え方については、複素数の基礎のページで解説しています)。
![]()
この合成インピーダンスZは、位相を考慮した、いわばベクトルのような表記になっています。もしこのインピーダンスZの大きさ(絶対値)を知りたければ、ベクトルの大きさを求めるのと同様に(ベクトルの大きさのページ参照)、三平方の定理を使って、次式で表すことができます。
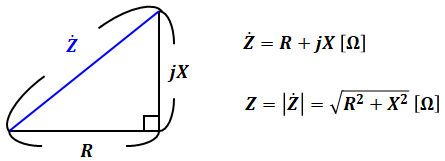
注意点として、上図では縦軸を「jX」としていますが、計算の際には「j」を抜いて「X」のみにしてください。
「jX」のまま2乗してしまうと、j2=-1なので「-X2」という値が出てしまいますが、大きさが負というのは有り得ません。ここでは虚数である目印として「j」を付けているだけなので、大きさを求める際には計算から外さなければいけません。
また、上図を見てもわかるように、実数と虚数はそれぞれ横軸と縦軸(x軸とy軸)に対応します。そのため、ベクトルの大きさを求めるときのように三角比の計算を使うパターンは生じず、複素数の場合は必ず、複素数の大きさを斜辺とし、実数と虚数を残る2辺とする直角三角形が成立します。
ちなみに、実数や虚数の符号(+or-)については特に気にする必要はありません。というのも、以下の式の通り、実数と虚数のどちらも2乗するため、最終的には必ず「+」になるからです。
![]()
![]()
![]()
![]()

コメント