電験三種 R6年度上期 理論 問13 問題と解説

　問 題　　　　　

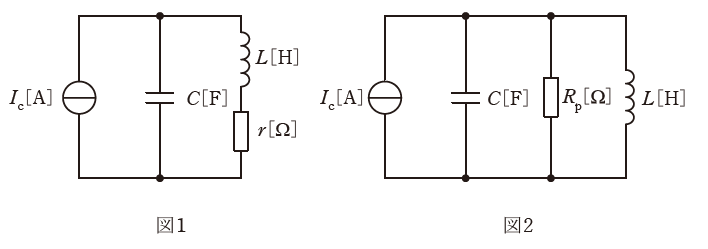
図1は、静電容量C[F]のコンデンサとコイルからなる共振回路の等価回路である。このようにコイルに内部抵抗r[Ω]が存在する場合は、インダクタンスL[H]と抵抗r[Ω]の直列回路として表すことができる。

この直列回路は、コイルの抵抗r[Ω]が、誘導性リアクタンスωL[Ω]に比べて十分小さいものとすると、図2のように、等価抵抗R_p[Ω]とインダクタンスL[H]の並列回路に変換することができる。

このときの等価抵抗R_p[Ω]の値を表す式として、正しいのは次のうちどれか。

ただし、I_c[A]は電流源の電流を表す。

1. ωL/r
2. r/(ωL)²
3. (ωL)²/r
4. r²/ωL
5. r(ωL)²

 

 

 

 

 

　解 説　　　　　

本問では、図1で直列に並んだrとLを描き換えたら、図2のような並列のR_pとLになったという話です。ここで、抵抗rの値はR_pに変わっていますが、インダクタンスLの値は変わっていないことがわかります。

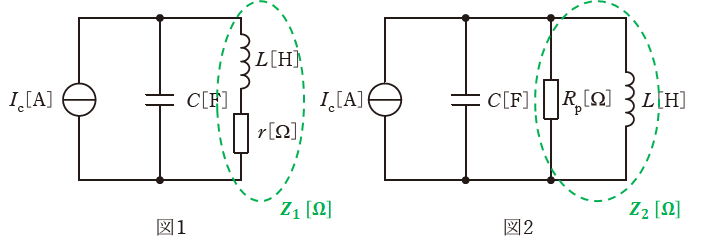
上図のように、図1のrとLを合わせた合成インダクタンスをZ₁[Ω]、図2のR_pとLを合わせた合成インダクタンスをZ₂[Ω]とすると、Z₁、Z₂はそれぞれ次の式で表すことができます。

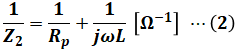
そして、上図で緑色の枠で囲った部分をひとまとまり(Z₁またはZ₂)と見なすと、図1も図2も全く同じ回路となるため、Z₁＝Z₂であることがわかります。よって、(1)式を(2)式に代入して数式を整理していくと、次のように書くことができます。

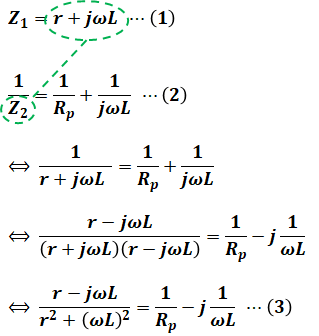
(3)式において、左辺の分母は「r²＋(ωL)²」となっていますが、問題文より「r≪ωL」であるため、この部分は「(ωL)²」に近似することができます。よって、(3)式は次に示す(4)式のように表すことができます。

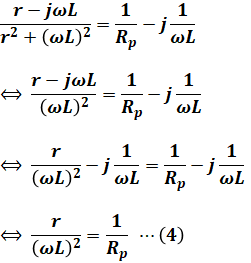
問われているのはR_pを表す式なので、(4)式をR_pについて解けば、求めたい答えが得られます。

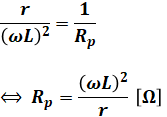
以上から、正解は(3)です。